Difference between revisions of "Manuals/calci/LISTPRIMES"
| Line 12: | Line 12: | ||
*<math>max </math> is the upper limit value and <math> min</math> is the lower limit value | *<math>max </math> is the upper limit value and <math> min</math> is the lower limit value | ||
*And <math> i</math> is the position of the prime number value. <math>i</math> value is optional. | *And <math> i</math> is the position of the prime number value. <math>i</math> value is optional. | ||
| − | *Suppose we are not giving the ith value, it will show all the prime numbers in given | + | *Suppose we are not giving the ith value, it will show all the prime numbers in given range. |
*This function will give the result as error when | *This function will give the result as error when | ||
| − | + | 1. any one of the argument is nonnumeric. | |
| − | + | 2.<math> max < min </math> or <math>i </math> is the beyond the range number of prime numbers | |
| − | + | 3.<math>max </math> or <math> min<0</math>. | |
| − | + | ==Examples== | |
| + | #LISTPRIMES(20,11)=11 13 17 19 | ||
| + | #LISTPRIMES(20,11,3)=17 | ||
| + | #LISTPRIMES(150,130)=131,137,139,149 | ||
| + | #LISTPRIMES(10,-1)=2 3 5 7 | ||
| + | #LISTPRIMES(-10,1)=Null | ||
| + | #LISTPRIMES(90,70)=71 73 79 83 89 | ||
| + | #LISTPRIMES(90,70,4)=83 | ||
| + | #LISTPRIMES(90,70,6)=Null | ||
| − | + | ==See Also== | |
| − | + | *[[Manuals/calci/INT | INT]] | |
| − | + | *[[Manuals/calci/EVEN | EVEN ]] | |
| − | + | *[[Manuals/calci/ODD | ODD ]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | [[ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Revision as of 02:50, 19 December 2013
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle max} is the upper limit,and
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle min} is the lower limit and i is the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} 'th position of a prime number.
Description
- This function is listing the set of prime numbers for the given set of numbers.
- A prime number is a natural number, it can be divided, without a remainder, only by itself and by 1.
- For e.g. the number 11 is a prime, because 11 is divided by 1 and 11 without any remainder.
- But 6 is not prime, because 6 can be divided by 1,2,3 and 6. Such numbers are called composite numbers.
- Also the number 0 and 1 are neither prime nor composite.
- In Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle LISTPRIMES(max,min,i)} , gives the list of prime numbers between the range Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle max } and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle min} .
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle max } is the upper limit value and is the lower limit value
- And Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} is the position of the prime number value. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} value is optional.
- Suppose we are not giving the ith value, it will show all the prime numbers in given range.
- This function will give the result as error when
1. any one of the argument is nonnumeric. 2.Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle max < min } or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i } is the beyond the range number of prime numbers 3.Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle max } or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle min<0} .
Examples
- LISTPRIMES(20,11)=11 13 17 19
- LISTPRIMES(20,11,3)=17
- LISTPRIMES(150,130)=131,137,139,149
- LISTPRIMES(10,-1)=2 3 5 7
- LISTPRIMES(-10,1)=Null
- LISTPRIMES(90,70)=71 73 79 83 89
- LISTPRIMES(90,70,4)=83
- LISTPRIMES(90,70,6)=Null
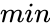 is the lower limit value
is the lower limit value