Difference between revisions of "Manuals/calci/LEVENESTEST"
Jump to navigation
Jump to search
| (26 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''LEVENESTEST( | + | <div style="font-size:30px">'''LEVENESTEST (DataRange,ConfidenceLevel,NewTableFlag)'''</div><br/> |
| − | *<math> | + | *<math>DataRange</math> is the set of values for the test. |
*<math>ConfidenceLevel</math> is the value from 0 to 1. | *<math>ConfidenceLevel</math> is the value from 0 to 1. | ||
| − | *<math> | + | *<math>NewTableFlag</math> is either TRUE or FALSE. TRUE for getting results in a new cube. FALSE will display results in the same cube. |
==Description== | ==Description== | ||
| Line 9: | Line 9: | ||
*Equal variances across samples is called homogeneity of variance or homoscedasticity. | *Equal variances across samples is called homogeneity of variance or homoscedasticity. | ||
*To do the Levenes test we need the following assumptions: | *To do the Levenes test we need the following assumptions: | ||
| − | 1.The Samples from the populations are | + | 1.The Samples from the populations are independent of one another. |
2. The population under consideration are Normally Distributed. | 2. The population under consideration are Normally Distributed. | ||
*For three or more variables the following statistical tests for homogeneity of variances are commonly used: | *For three or more variables the following statistical tests for homogeneity of variances are commonly used: | ||
| Line 17: | Line 17: | ||
*If the data surely is of normally distributed or nearly to normally distributed then we can use the Bartlett test. | *If the data surely is of normally distributed or nearly to normally distributed then we can use the Bartlett test. | ||
*The Levene's test is defined as | *The Levene's test is defined as | ||
| − | <math>H_0=\sigma_1^2=\sigma_2^2=......=\sigma_t^2</math>. | + | <math>H_0 = \sigma_1^2 = \sigma_2^2=...... = \sigma_t^2</math>. |
<math>H_1</math>=Not all of the variances are equal. | <math>H_1</math>=Not all of the variances are equal. | ||
*Normally there are three versions of the Levenes test. | *Normally there are three versions of the Levenes test. | ||
| − | *There are 1.Use of Mean.2.Use of Median.3.Use of 10% of Trimmed Mean. | + | *There are |
| + | *1.Use of Mean. | ||
| + | *2.Use of Median. | ||
| + | *3.Use of 10% of Trimmed Mean. | ||
*The Levene test statistic is: | *The Levene test statistic is: | ||
<math>W=\frac{(N-k)\sum_{i=1}^k N_i(Z_i-Z)^2}{(k-1)\sum_{i=1}^k \sum_{i=1}^k \sum_{j=1}^{N_i} (Z_{ij}-Z_i)^2}</math>. | <math>W=\frac{(N-k)\sum_{i=1}^k N_i(Z_i-Z)^2}{(k-1)\sum_{i=1}^k \sum_{i=1}^k \sum_{j=1}^{N_i} (Z_{ij}-Z_i)^2}</math>. | ||
| Line 26: | Line 29: | ||
**<math>k</math> is the number of different groups to which the sampled cases belong. | **<math>k</math> is the number of different groups to which the sampled cases belong. | ||
**<math>N</math> is the total number of cases in all groups. | **<math>N</math> is the total number of cases in all groups. | ||
| − | **<math>N_i</math> is the number of cases in the <math>i^th</math> group. | + | **<math>N_i</math> is the number of cases in the <math>i^{th}</math> group. |
| − | **<math>Y_{ij} is the value of the measured variable for the <math> | + | **<math>Y_{ij} is the value of the measured variable for the <math>j^{th}</math> case from the <math>i^{th}</math> group. |
*Zij is satisfying the one of the following conditions: | *Zij is satisfying the one of the following conditions: | ||
| − | *1.<math>z_{ij}=|y_{ij}-\bar{y_i}|</math>,Where <math>\bar{y_i}</math> is the Mean of the <math>i^th</math> subgroup. | + | *1.<math>z_{ij}=|y_{ij}-\bar{y_i}|</math>,Where <math>\bar{y_i}</math> is the Mean of the <math>i^{th}</math> subgroup. |
| − | *2.<math>z_{ij}=|y_{ij}-\bar{y_i}|</math>,Where <math>\bar{y_i}</math> is the Median of the <math>i^th</math> subgroup | + | *2.<math>z_{ij}=|y_{ij}-\bar{y_i}|</math>,Where <math>\bar{y_i}</math> is the Median of the <math>i^{th}</math> subgroup |
| − | *3.<math>z_{ij}=|y_{ij}-\bar{y_i}|</math>,Where <math>\bar{y_i}</math> is the 10%Trimmed Mean of the <math>i^th</math> subgroup. | + | *3.<math>z_{ij}=|y_{ij}-\bar{y_i}|</math>,Where <math>\bar{y_i}</math> is the 10%Trimmed Mean of the <math>i^{th}</math> subgroup. |
*Levene's Testing Procedure: | *Levene's Testing Procedure: | ||
*1. checking the assumptions. | *1. checking the assumptions. | ||
| Line 42: | Line 45: | ||
==Example== | ==Example== | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | X1 || X2 | ||
| + | |- | ||
| + | | 3067 || 3200 | ||
| + | |- | ||
| + | | 2730 || 2777 | ||
| + | |- | ||
| + | | 2840 || 2623 | ||
| + | |- | ||
| + | | 2913 || 3044 | ||
| + | |- | ||
| + | | 2789 || 2834 | ||
| + | |} | ||
| + | *=LEVENESTEST(B1:C5,.05,0) | ||
| + | {| class="wikitable" | ||
| + | |+LEVENES TEST | ||
| + | |- | ||
| + | ! !! DATA-0 !! DATA-1 | ||
| + | |- | ||
| + | | Median || 2840 || 2834 | ||
| + | |- | ||
| + | | Mean || 2867.8 || 2895.6 | ||
| + | |- | ||
| + | | Variance || 16923.7 || 51713.3 | ||
| + | |- | ||
| + | | Count || 5 || 5 | ||
| + | |- | ||
| + | | df || 4 || 4 | ||
| + | |} | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |+SUMMARY OUTPUT | ||
| + | |- | ||
| + | ! LEVENESTEST !! STATISTICS | ||
| + | |- | ||
| + | | W || 1.0439235110342522 | ||
| + | |- | ||
| + | | F-Test || 0.38245649772919 | ||
| + | |- | ||
| + | | a || 0.05 | ||
| + | |- | ||
| + | | F || 0.32726010523405 | ||
| + | |- | ||
| + | | p 1 & 2 Tail || 0.1524069466470822 || 0.3048138932941644 | ||
| + | |} | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|81Yi0cTuwzw|280|center|Levene's Test}} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/SIGNTEST| SIGNTEST]] | ||
| + | *[[Manuals/calci/FRIEDMANTEST| FRIEDMANTEST]] | ||
| + | |||
| + | |||
| + | ==References== | ||
| + | |||
| + | *[http://en.wikipedia.org/wiki/Levene%27s_test Levene's test documentation on Wikipedia] | ||
| + | *[http://www.qimacros.com/hypothesis-testing/levenes-test/ Levene's test for variance in Excel] | ||
Latest revision as of 15:57, 14 June 2018
LEVENESTEST (DataRange,ConfidenceLevel,NewTableFlag)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle DataRange} is the set of values for the test.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ConfidenceLevel} is the value from 0 to 1.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle NewTableFlag} is either TRUE or FALSE. TRUE for getting results in a new cube. FALSE will display results in the same cube.
Description
- This function used to test the Homogeneity of variances.
- Levene's test is used to test the Samples have equal variances.
- Equal variances across samples is called homogeneity of variance or homoscedasticity.
- To do the Levenes test we need the following assumptions:
1.The Samples from the populations are independent of one another. 2. The population under consideration are Normally Distributed.
- For three or more variables the following statistical tests for homogeneity of variances are commonly used:
1.Levene's Test. 2.Bartlett Test.
- Levene's test is an alternative to the Bartlett test.
- If the data surely is of normally distributed or nearly to normally distributed then we can use the Bartlett test.
- The Levene's test is defined as
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_0 = \sigma_1^2 = \sigma_2^2=...... = \sigma_t^2}
.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_1}
=Not all of the variances are equal.
- Normally there are three versions of the Levenes test.
- There are
- 1.Use of Mean.
- 2.Use of Median.
- 3.Use of 10% of Trimmed Mean.
- The Levene test statistic is:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W=\frac{(N-k)\sum_{i=1}^k N_i(Z_i-Z)^2}{(k-1)\sum_{i=1}^k \sum_{i=1}^k \sum_{j=1}^{N_i} (Z_{ij}-Z_i)^2}} .
- where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W} is the result of the test.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} is the number of different groups to which the sampled cases belong.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} is the total number of cases in all groups.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N_i} is the number of cases in the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i^{th}} group.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y_{ij} is the value of the measured variable for the <math>j^{th}} case from the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i^{th}} group.
- Zij is satisfying the one of the following conditions:
- 1.Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_{ij}=|y_{ij}-\bar{y_i}|} ,Where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bar{y_i}} is the Mean of the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i^{th}} subgroup.
- 2.Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_{ij}=|y_{ij}-\bar{y_i}|} ,Where is the Median of the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i^{th}} subgroup
- 3.Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_{ij}=|y_{ij}-\bar{y_i}|} ,Where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bar{y_i}} is the 10%Trimmed Mean of the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i^{th}} subgroup.
- Levene's Testing Procedure:
- 1. checking the assumptions.
- 2.State the Null(H0) and alternative(H1) hypothesis.
- 3.Decide on the Significance level (α).
- 4.Finding the Critical value and Rejection Region.Here Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle df_1=t-1} ,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle df_2=N-t} .
- 5.Compute the Levenes statistic using the formula.
- 6.Then decision of the value of the test statistic,W is falls in the rejection region or if p-value ≤ α, then reject Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_0} .Otherwise, fail to reject Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_0} . For the computation p-value we have to use the value of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle df_1} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle df_2} .
- 7. Finally we have to conclude that the rejection of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_0} or fail to rejection Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_0} according to the test statistic at the significance level.
Example
| X1 | X2 |
| 3067 | 3200 |
| 2730 | 2777 |
| 2840 | 2623 |
| 2913 | 3044 |
| 2789 | 2834 |
- =LEVENESTEST(B1:C5,.05,0)
| DATA-0 | DATA-1 | |
|---|---|---|
| Median | 2840 | 2834 |
| Mean | 2867.8 | 2895.6 |
| Variance | 16923.7 | 51713.3 |
| Count | 5 | 5 |
| df | 4 | 4 |
| LEVENESTEST | STATISTICS | |
|---|---|---|
| W | 1.0439235110342522 | |
| F-Test | 0.38245649772919 | |
| a | 0.05 | |
| F | 0.32726010523405 | |
| p 1 & 2 Tail | 0.1524069466470822 | 0.3048138932941644 |
Related Videos
See Also
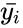 is the Median of the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i^{th}}
subgroup
is the Median of the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i^{th}}
subgroup