Difference between revisions of "RvsZ3"
| Line 794: | Line 794: | ||
| − | In Z3, QRDECOMPOSITION() | + | In Z3, QRDECOMPOSITION() calculates the product of orthogonal matrix and upper triangular matrix. |
{| class="wikitable" | {| class="wikitable" | ||
| Line 820: | Line 820: | ||
-1.1102230246251565e-15 -8.825226081218279 | -1.1102230246251565e-15 -8.825226081218279 | ||
|} | |} | ||
| − | |||
| − | |||
===Forming partitioned matrices=== | ===Forming partitioned matrices=== | ||
Revision as of 05:47, 26 July 2021
Comparison of R and Z3
Simple manipulations; numbers and vectors
Vectors and assignment
Z3 operates on named data structures. The simplest such structure is the numeric vector, which is a single entity consisting of an ordered collection of numbers.
To set up a vector named x, say, consisting of five numbers, namely 10.4, 5.6, 3.1, 6.4 and 21.7, use the R command
> x <- c(10.4, 5.6, 3.1, 6.4, 21.7)
Z3 command to set up a vector is:
x<==[10.4, 5.6, 3.1, 6.4, 21.7];
Alternatively we can use the simple "=" also.
x=[10.4, 5.6, 3.1, 6.4, 21.7]
Assignment can also be made using the function ASSIGN(). An equivalent way of making the same assignment as above is with:
In R,
> assign("x", c(10.4, 5.6, 3.1, 6.4, 21.7))
In Z3, use the "ASSIGN" function as:
ASSIGN("x", [10.4, 5.6, 3.1, 6.4, 21.7])
Assignments can also be made in the other direction, using the obvious change in the assignment operator. So the same assignment could be made using
[10.4, 5.6, 3.1, 6.4, 21.7]==>x
The reciprocals of the above five values for x in R,
> 1/x
In Z3, We can use the function called Reciprocal,
RECIPROCAL(x) (the value of x is [10.4, 5.6, 3.1, 6.4, 21.7]
Also we can use directly,
([10.4,5.6,3.1,6.4,21.7]<>d40)@(x=>1/x)
The further assignment
> y <- c(x, 0, x)
would create a vector y with 11 entries consisting of two copies of x with a zero in the middle place.
Vector arithmetic
Vectors can be used in arithmetic expressions, in which case the operations are performed element by element. Vectors occurring in the same expression need not all be of the same length. If they are not, the value of the expression is a vector with the same length as the longest vector which occurs in the expression. So with the above assignments the R command
> v <- 2*x + y + 1
generates a new vector v of length 11 constructed by adding together, element by element, 2*x repeated 2.2 times, y repeated just once, and 1 repeated 11 times.
With the same Assignment Z3 command is.
v=2*x+y+1
In Z3 the elementary arithmetic operators are the usual +, -, *, / and ^ for raising to a power. Also we can use the functions SUM,SUB,PRODUCT,DIVIDE and POWER instead of using arithmetic operators.
In addition all of the common arithmetic functions are available. LOG, EXP, SQRT, SIN, COS, TAN, SEC,COSEC,COTAN, Hyperbolic functions and so on. For trignometric functions we can find the values in Deg and Radians also.
MAX and MIN select the largest and smallest elements of a vector respectively.
In R,two statistical functions are mean(x) which calculates the sample mean, which is the same as sum(x)/length(x), and var(x) which gives
sum((x-mean(x))^2)/(length(x)-1)
or sample variance.
In Z3,to find the mean value we can use function called MEAN(x), AVG(x) or AVERAGE(x).
In R, sort(x) returns a vector of the same size as x with the elements arranged in increasing order.
SORTING(x) returns the vector in increasing order in Z3.
The parallel maximum and minimum functions pmax and pmin return a vector that contains in each element the largest\smallest element in that position in any of the input vectors.
In Z3, we can apply any function for each cell,row and column.
Array.$(Function) - Apply any function to each element Array.$$(Function) - Apply any function to each row Array.$$(Function) - Apply any function to each column.
Also to find the parallel min and max we can use the below function in Z3.
PMAX(MS(15)) PMIN(MS(15)) PMAX(MS(15),SUM) - This can be used to override MIN and MAX with another function PMIN(MS(15),SUM)
To work with complex numbers, supply an explicit complex part. Thus sqrt(-17) will give NaN and a warning, but sqrt(-17+0i) will do the computations as complex numbers in R.
In Z3, while computing complex numbers simply we can use as
SQRT(-17) or SQRT(-17+0i).
Generating regular sequences
The function seq() is a more general facility for generating sequences. To get the sequence of values from a particular range with step value with R as
> seq(-5, 5, by=.2) -> s3
generates in s3 the vector c(-5.0, -4.8, -4.6, ..., 4.6, 4.8, 5.0).
Similarly
> s4 <- seq(length=51, from=-5, by=.2)
generates the same vector in s4.
Z3 command to get a sequence value as:
s3=-5..5..0.2
generates in s3 vector.
s4=Array(51).seq(-5,0.2)
generates s4 vector with same as s3.
To print the five copies of x end-to-end in s5 the R command is
> s5 <- rep(x, times=5)
Alternatively
> s6 <- rep(x, each=5)
which repeats each element of x five times before moving on to the next.
The z3 command of replicating the array value is:
s5=x.replicate(5)
The another way is:
s6=RECURSIVEARRAY(5,x)
Logical vectors
The elements of a logical vector can have the values TRUE, FALSE, and NA. Logical vectors are generated by conditions.
For example
> temp <- x > 13 sets temp as a vector of the same length as x with values FALSE corresponding to elements of x where the condition is not met and TRUE where it is.
Z3 command to generate the logical vector is:
[10.4,5.6,3.1,6.4,21.7]|[x,x>13]|;
Logical vectors may be used in ordinary arithmetic, in which case they are coerced into numeric vectors, FALSE becoming 0 and TRUE becoming 1.
Missing values
The function is.na(x) gives a logical vector of the same size as x with value TRUE if and only if the corresponding element in x is NA.
> z <- c(1:3,NA); ind <- is.na(z)
Z3 command for ISNA is:
z=([1,2,3,"NA"]);ISNA(z)
There is a second kind of “missing” values which are produced by numerical computation, the so-called Not a Number, NaN, values. In R, examples are
> 0/0
or
> Inf - Inf which both give NaN since the result cannot be defined sensibly.
In z3,
0/0 will give the result as NaN.
∞-∞; \\Symbol of Infinity
will give the result as Null.
Character vectors
Character quantities and character vectors are used frequently in R, for example as plot labels. The paste() function takes an arbitrary number of arguments and concatenates them one by one into character strings.
The arguments are by default separated in the result by a single blank character, but this can be changed by the named parameter, sep=string, which changes it to string, possibly empty.
For example,
> labs <- paste(c("X","Y"), 1:10, sep="")
makes labs into the character vector
c("X1", "Y2", "X3", "Y4", "X5", "Y6", "X7", "Y8", "X9", "Y10")
Z3 command to execute the above is:
|10|.fillwith("x","y").joincolumnswith(1..10) //need to add " " symbol in its result
Index vectors; selecting and modifying subsets of a data set
Subsets of the elements of a vector may be selected by appending to the name of the vector an index vector in square brackets. Such index vectors can be any of four distinct types.
- A logical vector:
Values corresponding to TRUE in the index vector are selected and those corresponding to FALSE are omitted. For example > y <- x[!is.na(x)] creates (or re-creates) an object y which will contain the non-missing values of x, in the same order. Note that if x has missing values, y will be shorter than x. Also > (x+1)[(!is.na(x)) & x>0] -> z
Corresponding z3 command is:
y = x(!=ISNA(x))
To create z is:
z=(x+1)[(!ISNA(x)) & x>0]
Also we can use the symbol in Z3 for the above function is != For Example
1..10|!=|1..130 - Will give the result as true or false.
- A vector of positive integral quantities:
The corresponding elements of the vector are selected and concatenated, in that order, in the result. In R, x[6] is the sixth component of x and > x[1:10] The same in Z3 command is:
x.any(10) //Need to check
selects the first 10 elements of x (assuming length(x) is not less than 10). Also > c("x","y")[rep(c(1,2,2,1), times=4)]
- A vector of negative integral quantities:
Such an index vector specifies the values to be excluded rather than included. Thus > y <- x[-(1:5)] gives y all but the first five elements of x. \\it is not showing the first five elements of x. It is just showing the result as numeric(0)
Z3 command to index vector specification is:
// To include
- A vector of character strings:
In this case a sub-vector of the names vector may be used in the same way as the positive integral labels in item 2 further above.
> fruit <- c(5, 10, 1, 20) > names(fruit) <- c("orange", "banana", "apple", "peach") > lunch <- fruit[c("apple","orange")]
The advantage is that alphanumeric names are often easier to remember than numeric indices.
The same in Z3 command is:
fruit=[5, 10, 1, 20] ["names"]<<<"orange", "banana", "apple", "peach" //Here names(fruit) is not giving result ["lunch"] <<<fruit[("apple","orange")] // Giving the result as null
The vector assigned must match the length of the index vector, and in the case of a logical index vector it must again be the same length as the vector it is indexing. For example > x[is.na(x)] <- 0
replaces any missing values in x by zeros and > y[y < 0] <- -y[y < 0]
has the same effect as > y <- abs(y)
We can write in Z3,
x[ISNA(x)] = 0
Replacing values in x is:
y[y < 0] = -y[y < 0]
Also we can write as,
y = ABS(y)
Objects, their modes and attributes
Intrinsic attributes: mode and length
R consists of a number of data objects to perform various functions. There are 6 types of objects in R Programming. They include vector, list, matrix, array, factor, and data frame.
Vectors in R programming data objects: logical, integer, character, raw, double, and complex.
Z3 language also supports data objects: logical, integer, character, raw, double, and complex.
Lists in R contain various types of elements including strings, numbers, vectors, and a nested list inside it. It can also consist of matrices or functions as elements. It can be created with the help of the list() function.
Z3 stores all the data in array format. The data can be strings, numbers, vectors, matrices or functions as elements.
List of elements can be displayed using Z3 command LISTALL.
Matrices in R Programming are used to arrange elements in the two-dimensional layout to perform mathematical operations.
Matrices in Z3 can be of any dimensions. A matrix can be defined in many ways such as:
MATRIX(3) //Displays 3x3 matrix
or
MATRIX("anti-diagonal",4,200..204) //Displays 4x4 anti-diagonal matrix with values in between 200 and 204
or
|5| //Displays 5x5 matrix
or
|2,3,4| //Displays 2x3x4 matrix
An array in R is used to store data in multi-dimensional format. It can be created with the help of an array() function.
Z3 has n number of commands for using array functions such as:
ARRAY(3,4) //Defines a 3-dimensional array with each element value of 4
a=[[1,3,4],[2,3,4]] //Defines an array 'a' a.add(45) //Adds 45 in each array element
Row, Column, Diagonal, concatination etc operations are possible using Z3 commands. (Refer list of Array Manipulation Functions here: https://wiki.zcubes.com/Z%5E3_Array_Manipulation_Member_Functions)
Factors are data objects that are used in order to categorize and store data as levels. They can be strings or integers. They are extremely useful in data analytics for statistical modeling. They can be created using factor() function.
Factors can be identified or retrieved in Z3 by giving variable name as a command.
a=[[11,3,4],[21,3,4]] //Defines array 'a' a //Displays elements of array 'a'
Dataframe is a 2-dimensional data structure wherein each column consists of the value of one variable and each row consists of a value set from each column.
.................Need to add explanation for this..............................
Properties of an object are provided by attributes such as mode, length.
In R, change of mode is represented as:
> z <- 0:9 //z is defined with elements 0 to 9
> digits <- as.character(z) // digits is the character vector c("0", "1", "2", ..., "9")
> d <- as.integer(digits) //Now d and z are the same
In Z3, the above mode change can be represented as:
z=[0..9] digits=CHAR(z) d= INT(digits)
Changing the length of an object
In R language, an “empty” object can be defined as:
> e <- numeric() //makes e an empty vector structure of mode numeric.
> e <- character() //makes e an empty vector structure of mode character.
Using below Z3 command, an empty object can be defined as:
e=NUM() e=CHAR()
Once an object of any size has been created, new components may be added to it simply by giving it an index value outside its previous range.
In R,
> e[3] <- 17 //makes e a vector of length 3
Z3 command is:
e[3]=17 //length of e vector is 3
In R, the length of a vector can be retrieved by R command:
>length(e)
Z3 command used is:
LEN(e) //displays output as 3
Getting an setting attributes
R command:
attr(z, "dim") <- c(10,10)
Z3 command:
to do ***
The class of an object
Object in R with class "data.frame", plot() and other functions such as summary() will display the output values in certain ways. Using Z3, the data output values can be displayed in list format, spreadsheet format, graphical format etc.
In R, unclass() removes temporarily the effects of class. For example if winter has the class "data.frame" then
> winter
will print it in data frame form, which is rather like a matrix, whereas
> unclass(winter)
will print it as an ordinary list.
In Z3,
' to do *** '
Ordered and unordered factors
A factor is a vector object used to specify a discrete classification (grouping) of the components of other vectors of the same length.
A specific example
A sample of 30 tax accountants from all the states and territories of Australia and their individual state of origin is specified by a character vector of state mnemonics: In R,
> state <- c("tas", "sa", "qld", "nsw", "nsw", "nt", "wa", "wa",
"qld", "vic", "nsw", "vic", "qld", "qld", "sa", "tas",
"sa", "nt", "wa", "vic", "qld", "nsw", "nsw", "wa",
"sa", "act", "nsw", "vic", "vic", "act")
In R, a factor is similarly created using the factor() function as:
> statef <- factor(state)
In R, the print() function handles factors slightly differently from other objects:
> statef
Output in R,
[1] tas sa qld nsw nsw nt wa wa qld vic nsw vic qld qld sa [16] tas sa nt wa vic qld nsw nsw wa sa act nsw vic vic act Levels: act nsw nt qld sa tas vic wa
In R, to find out the levels of a factor the function levels() can be used.
> levels(statef)
Output in R,
[1] "act" "nsw" "nt" "qld" "sa" "tas" "vic" "wa"
...' to do ***'....Z3 equivalent commands to be added
The function tapply() and ragged arrays
To continue the previous example, suppose we have the incomes of the same tax accountants in another vector (in suitably large units of money)
> incomes <- c(60, 49, 40, 61, 64, 60, 59, 54, 62, 69, 70, 42, 56, 61, 61, 61, 58, 51, 48, 65, 49, 49, 41, 48, 52, 46, 59, 46, 58, 43)
To calculate the sample mean income for each state, tapply() function is used in R:
> incmeans <- tapply(incomes, statef, mean) giving a means vector with the components labelled by the levels act nsw nt qld sa tas vic wa 44.500 57.333 55.500 53.600 55.000 60.500 56.000 52.250
Sample variance is calculated in R as:
> stderr <- function(x) sqrt(var(x)/length(x))
Standard errors in R are calculated as:
> incster <- tapply(incomes, statef, stderr)
and the values calculated are then
> incster
act nsw nt qld sa tas vic wa 1.5 4.3102 4.5 4.1061 2.7386 0.5 5.244 2.6575
The combination of a vector and a labelling factor is an example of what is sometimes called a ragged array, since the subclass sizes are possibly irregular.
...' to do ***'....Z3 equivalent commands to be added
Ordered factors
The levels of factors are stored in alphabetical order, or in the order they were specified to factor if they were specified explicitly. Sometimes the levels will have a natural ordering that we want to record and want our statistical analysis to make use of. The ordered() function creates such ordered factors but is otherwise identical to factor.
...' to do ***'....Z3 explanation to be added here
Arrays and Matrices
Arrays
In R, a 3 by 5 by 100 dimension vector z of 1500 elements is defined as:
> dim(z) <- c(3,5,100)
In Z3, command to define an array is:
DIM(3,5,100)
Alternatively it can also be represented in array form as:
|3,5,100|
Array indexing. Subsections of an array
In R, a 4 x 2 array with array elements is represented as:
c(a[2,1,1], a[2,2,1], a[2,3,1], a[2,4,1], a[2,1,2], a[2,2,2], a[2,3,2], a[2,4,2])
In Z3, the above 4 X 2 array with array elements is defined using square brackets as:
[[2,1,1], [2,2,1], [2,3,1], [2,4,1], [2,1,2], [2,2,2], [2,3,2], [2,4,2]]
The above array can be stored with a variable name 'Z' as:
z = [[2,1,1], [2,2,1], [2,3,1], [2,4,1], [2,1,2], [2,2,2], [2,3,2], [2,4,2]]
The contents of variable Z can be obtained using Z3 command:
DIM(z)
Also, to identify the size of 'z', use the Z3 command:
DIMENSIONS(z)
which gives the result as: 8 3 (8 rows, 3 columns)
Index matrices
In R, a matrix 'x' with 4 rows and 5 colums containing values from 1 to 20, is defined as:
> x <- array(1:20, dim=c(4,5))
This command displays the result as:
[,1] [,2] [,3] [,4] [,5] [1,] 1 5 9 13 17
[2,] 2 6 10 14 18
[3,] 3 7 11 15 19
[4,] 4 8 12 16 20
The Z3 command can be used as:
x= |4,5,1..20|
In Z3, the array elements are stored row wise.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
' to do *** ' : Z3 command to be added to obtain same output as in R
Array function
Array function in R:
> Z <- array(data_vector, dim_vector)
For example
> Z <- array(h, dim=c(3,4,2)) same as > Z <- h ; dim(Z) <- c(3,4,2)
> Z <- array(0, c(3,4,2)) //makes Z an array of all zeros.
Z3 Commands used are:
z=[3,4,2] //Defines an array z with elements specified
REPLACE(z,0) //Replaces elements in z with '0'
So if A, B and C are all similar arrays, then D is a similar array with its data vector being the result of the given element-by-element
operations.
R command:
> D <- 2*A*B + C + 1
Z3 command:
d= 2*a*b+c+1
The outer product of two arrays
In R language, if a and b are two numeric arrays, their outer product is formed by the special operator %o%:
> ab <- a %o% b or also alternatively, > ab <- outer(a, b, "*")
In Z3, array can be multiplied using inbuilt '.multiply' function. e.g
[[1,3,4],[2,3,4]].multiply(45)
Multiplication of two or more matrices can be carried using Z3 commands:
MATRIXMULTIPLY([2,-3,4;-5,6,7],9) or MATRIXPRODUCT([2,3,4;5,6,7],5) or MATRIXPRODUCT([[6,7,8],[10,12,-22],[7,17,23]],[[20,12,16],[7,8,13],[4,8,9]])
In R, the multiplication function can be replaced by an arbitrary function of two variables as:
> f <- function(x, y) cos(y)/(1 + x^2) > z <- outer(x, y, f)
In Z3, the above function can be defined as:
f(x,y)=COS(y)/(1+x^2) ...' to do *** '............
Refer all array manipulation functions here: Listing of Z3 Array Manipulation Member Functions
Generalized transpose of an array
In R language, transpose of an array can be calculated using aperm() or t() functions as:
> B <- aperm(A, c(2,1)) or B <- t(A)
In Z3 language, transpose can be calculated using commands array.flip(),t(), MATRIXTRANSPOSE() functions as:
[[1,8,3],[7,4,5],[9,13,45]].flip() or MAGICSQUARE(3).t() or MATRIXTRANSPOSE([[12,17,18],[6,15,36],[13,19,25]])
Matrix facilities
R has matrix functions such as:
t(X) is the matrix transpose nrow(A) gives number of rows in the matrix A ncol(A) give the number of columns in the matrix A
Z3 has number of matrix functions such as:
MATRIXTRANSPOSE() returns transpose of a matrix MATRIXROW returns specified row elements MATRIXCOLUMN returns specified column elements
To know more matrix functions, read here: [| Matrix Functions 1] [| Matrix Functions 2]
Matrix multiplication
In R, the operator %*% is used for matrix multiplication. If, for example, A and B are square matrices of the same size, then
> A * B is the matrix of element by element products and > A %*% B is the matrix product. If x is a vector, then > x %*% A %*% x is a quadratic form
In Z3, functions such as MATRIXMULTIPLY() or MMULT() are used for matrix multiplication
e.g 1 MATRIXMULTIPLY([4,7.2,6;9,-8,12],[2,3;6,5;9,8])
e.g 2 MMULT([[2.5,4,3,7],[1,3,5,4]],[[2,5,6],[7.3,4,9],[10,4,1],[6,2,8]])
Function crossprod() in R language forms crossproducts of two matrices.
In R,
x<- matrix(1:4,2,2) crossprod(x)
displays the output as:
[,1] [,2] [1,] 5 11 [2,] 11 25
In Z3, functions such as CROSSPRODUCT() and VECTORPRODUCT() are used.
CROSSPRODUCT([2,7,8],[3,9,5]) =-37 14 -3 or VECTORPRODUCT([2,3,5],[8,6,4]) = -18 32 -12
IN R, diag(v) displays diagonal elements of vector v.
x <- matrix(1:4, 2, 2) diag(x)
displays the output as:
[1] 1 4
In Z3, DIAG() function is used to display diagonal elements as:
DIAG([[1,2],[3,4]]) displays result as 1,4
DIAG([[21,43,-56],[1,-6,-15],[2,3.2,8]]) displays result as 21, -6, 8
Linear equations and inversion
In R, solving linear equations is the inverse of matrix multiplication.
> b <- A %*% x
If only A and b are given, the vector x is the solution of that linear equation system. In R,
> solve(A,b)
solves the system, returning x (up to some accuracy loss). Note that in linear algebra, formally x = A−1b where A−1 denotes the inverse of A, which can be computed by solve(A)
x <- solve(A) %*% b
or
>solve(A,b)
The quadratic form x can be calculated as:
x %*% solve(A,x)
In Z3, if a ,b and r are real numbers also a and b are not equal to 0,then ax+by=r is called a linear equation in two variables. Function LINEAREQUATION() can be used directly to find linear equation between two variables.
e.g LINEAREQUATION([[1,1,5],[1,-1,3]]) = 4 1
In Z3, the inverse of a matrix can be calculated using MINVERSE() or MATRIXINVERSE() functions.
MINVERSE([[10,12],[11,14]])
or
MATRIXINVERSE([4,7;2,6])
Eigenvalues and eigenvectors
In R, the function eigen(Sm) calculates the eigenvalues and eigenvectors of a symmetric matrix Sm.
> ev <- eigen(Sm)
will assign this list to ev. Then ev$val is the vector of eigenvalues of Sm and ev$vec is the matrix of corresponding eigenvectors.
In Z3, eigen values of a given matrix is calculated as:
| A | B | C | |
|---|---|---|---|
| 1 | 3 | 7 | 5 |
| 2 | 10 | 12 | 8 |
| 3 | 6 | 8 | 14 |
=EIGENVALUES(A1:C3)
-2.018987498930866 |
25.303239119591886 |
5.715748379338994 |
-0.8195524172935329 0.3557792393359474 0.2128903683040517 |
0.5726193656991498 0.663334322125492 0.6212592923173481 |
0.02099755544415341 0.6583378387635402 -0.7541316747045657 |
Singular value decomposition and determinants
In R, the function svd(M) takes an arbitrary matrix argument, M, and calculates the singular value decomposition of M. This consists of a matrix of orthonormal columns U with the same column space as M, a second matrix of orthonormal columns V whose column space is the row space of M and a diagonal matrix of positive entries D such that
M = U %*% D %*% t(V)
D is actually returned as a vector of the diagonal elements.
For square matrix,
> absdetM <- prod(svd(M)$d)
calculates the absolute value of the determinant of M.
In Z3, there are multiple inbuilt functions such as SVF(), SVD(), QRDECOMPOSTION(), LUDECOMPOSITION(), MATRIXDECOMPOSE() etc. to calculate decomposition values of given matrix. e.g
| A | B | C | |
|---|---|---|---|
| 1 | 1 | 0 | 1 |
| 2 | -1 | -2 | 0 |
| 3 | 0 | 1 | -1 |
=SVD(A1:C3)
0.12000026038175768 -0.8097122815927454 -0.5744266346072238 |
-0.9017526469088556 0.15312282248412068 -0.40422217285469236 |
0.41526148545366265 0.5664975042066532 -0.7117854145923829 |
2.4605048700187635 0 0 |
0 1.699628148275319 0 |
0 0 0.23912327825655444 |
0.4152614854539272 -0.566497504206459 -0.711854145923831 |
0.9017526469087841 0.15312282248454143 0.4042221728546923 |
-0.12000026038137995 -0.8097122815928015 0.5744266346072238 |
For more information on decomposition functions, read here:
- [|SVD]
- [|LUDECOMPOSITION ]
- [|QRDECOMPOSITION ]
- [|SVF]
- [|MATRIXDECOMPOSE]
Least squares fitting and the QR decomposition
In R, the function lsfit() returns a list giving results of a least squares fitting procedure. An assignment such as
> ans <- lsfit(X, y)
gives the results of a least squares fit where y is the vector of observations and X is the design matrix.
' to do *** '-------------------need to add Z3 command equivalent to lsfit .
In R, another closely related function is qr() and its allies. Consider the following assignments
> Xplus <- qr(X) > b <- qr.coef(Xplus, y) > fit <- qr.fitted(Xplus, y) > res <- qr.resid(Xplus, y)
These compute the orthogonal projection of y onto the range of X in fit, the projection onto the orthogonal complement in res and the coefficient vector for the projection in b.
In Z3, QRDECOMPOSITION() calculates the product of orthogonal matrix and upper triangular matrix.
| A | B | |
|---|---|---|
| 1 | 2 | 6 |
| 2 | 10 | -15 |
=QRDECOMPOSITION(A1:B2)
-0.19611613513818393 -0.9805806756909202 |
-0.9805806756909202 0.19611613513818393 |
-10.19803902718557 13.5320133245347 |
-1.1102230246251565e-15 -8.825226081218279 |
Forming partitioned matrices
Matrices can be built up from other vectors and matrices by the functions cbind() and rbind(). Roughly cbind() forms matrices by binding together matrices horizontally, or column-wise, and rbind() vertically, or row-wise. In R language, cbind() and rbind() are used as below:
> X <- cbind(arg_1, arg_2, arg_3, ...)
The function rbind() does the corresponding operation for rows.
Z3 has inbuilt functions such as MATRIXJOIN(), MATRIXAPPENDROWS(), MATRIXAPPENDCOLUMNS() can be used to append/bind the columns/rows in a single matrix. e.g
MATRIXJOIN([2,7,6;4,5,6],[3,5,4;9,6,1])
or
MATRIXAPPENDCOLUMNS([2,3,4;7,8,9;10,2,4],[4,6,9;20,22,43;17,13,19])
or
MATRIXAPPENDROWS([2,3;4,5],[8,7;9,3])
Suppose X1 and X2 have the same number of rows. These can be combined by columns into a matrix X, together with an initial column of 1s as:
R command:
> X <- cbind(1, X1, X2)
Z3 command:
x= MATRIXAPPENDROWS([1;1],[2,3;4,5],[8,7;9,3])
The concatenation function c() with arrays
R language uses the following command to coerce an array back to a simple vector object:
> vec <- as.vector(X)
or
> vec <- c(X)
MERGE(), MERGEROWS(), MERGECOLUMNS(), MERGEIO(), Array.x$, Array.$x are various inbuilt Z3 functions to concatenate elements with a given array.
Please refer Z3 functions: *[| Merge functions] *[| Array.x$]
Frequency tables from factors
Suppose, for example, that statef is a factor giving the state code for each entry in a data vector. R command:
> statefr <- table(statef)
gives in statefr a table of frequencies of each state in the sample.
Further suppose that incomef is a factor giving a suitably defined “income class” for each entry in the data vector, for example with the cut() function:
> factor(cut(incomes, breaks = 35+10*(0:7))) -> incomef
Then to calculate a two-way table of frequencies:
> table(incomef,statef)
' to do *** '-------------------need to add Z3 equivalent command
Lists and data frames
Lists
An R list is an object consisting of an ordered collection of objects known as its components.
An Example to make a list is: > Lst <- list(name="Fred", wife="Mary", no.children=3,child.ages=c(4,7,9))
An Example in Z3 is:
Lst=[name="Fred",wife="Mary",NoofChildren=3,Childages=[4,7,9]];
To know the number of component it has in R, length(Lst)
Lst.length gives the number of component in Z3.
Components of lists may also be named, > name$component_name
**To do for Z3
Simple Example to get the right component in R:
Lst$name is the same as Lst1 and is the string "Fred"
Lst$wife is the same as Lst2 and is the string "Mary"
Lst$child.ages[1] is the same as Lst4[1] and is the number 4
Also Lst"name" is the same as Lst$name.
The same result will get in Z3,
name or Lst0 wife or Lst1 Childages or Lst3 and the result as 4,7,9
Also we can use,
name@Lst //To check this format result
When the name of the component to be extracted is stored in another variable in R as, > x <- "name"; Lstx
In Z3,
x=["name"];x@Lst;
The names of components may be abbreviated down to the minimum number of letters needed to identify them uniquely. Thus Lst$coefficients may be minimally specified as Lst$coe and Lst$covariance as Lst$cov.
In Z3, we can use the COVAR@Lst instead of COVARIANCE@Lst.
Constructing and modifying lists
New lists may be formed from existing objects by the function list(). An assignment of the form > Lst <- list(name_1=object_1, ..., name_m=object_m) \\not giving any result in R
- To do the same in Z3.
Lists, like any subscripted object, can be extended by specifying additional components.
For example > Lst[5] <- list(matrix=Mat) \\Not giving any result
- To do in Z3.
Concatenating lists
We can joined together all arguments into a single vector structure using concatenate in R.
> list.ABC <- c(list.A, list.B, list.C)
In Z3,we can use concatenate function in two ways:
CONCATENATE("Happy"," ","Holidays!")
or
CONCAT("Happy"," ","Holidays!")
To know more on Array concatenate functions in: [|Array-Concatenate]
Making data frames
A list whose components conform to the restrictions of a data frame may be coerced into a data frame using the function as.data.frame()
> accountants <- data.frame(home=statef, loot=incomes, shot=incomef) \\Not giving any result
**To do the same in Z3.
attach() and detach()
To attach a database as a list or data frame as its argument we can use the function called attach() in R Thus suppose lentils is a data frame with three variables lentils$u, lentils$v,lentils$w.
> attach(lentils)
** To do in Z3.
Attaching arbitrary lists
Any object of mode "list" may be attached in R as,
> attach(any.old.list)
- Z3 command to include
Managing the search path
The way to keep a track of data frames and lists are attached in R as,
> search() [1] ".GlobalEnv" "Autoloads" "package:base"
Also to detach the data frame and confirm it has been removed from the search path. > detach("lentils") > search() [1] ".GlobalEnv" "Autoloads" "package:base"
*** To do the equivalent in Z3.
Reading data from files
The read.table() function
To read the data frame directly in R use the read.table() function.
For Example,
> HousePrice <- read.table("houses.data")
To omit including the row labels directly and use the default labels. The data frame may then be read as
> HousePrice <- read.table("houses.data", header=TRUE)
- To do in Z3
The scan() function
The scan() function to read in the three vectors as a list, as follows in R
> inp <- scan("input.dat", list("",0,0))
To separate the data items into three separate vectors, use assignments like
> label <- inp1; x <- inp2; y <- inp3
If the second argument is a single value and not a list, a single vector is read in, all components of which must be of the same mode as the dummy value.
> X <- matrix(scan("light.dat", 0), ncol=5, byrow=TRUE)
- to do in Z3
Accessing builtin datasets
List of datasets in R,
data() As from R version 2.0.0 all the datasets supplied with R are available directly by name.
- To do in Z3.
Loading data from other R packages
To access data from a particular package, use the package argument, for example
data(package="rpart")
data(Puromycin, package="datasets")
- To do in Z3.
Probability distributions
R as a set of statistical tables
The below are list of distributions and its name in R and Z3.
| Distribution | R Name | Z3 Name |
|---|---|---|
| beta | beta | BETADIST |
| binomial | binom | BINOMDIST |
| Cauchy | cauchy | |
| chi-squared | chisq | CHIDIST |
| exponential | exp | EXP |
| F | f | FDIST |
| gamma | gamma | GAMMADIST |
| geometric | geom | |
| hypergeometric | hyper | HYPGEOMDIST |
| log-normal | lnorm | LOGNORMDIST |
| logistic | logis | |
| negative binomial | nbinom | NEGBINOMDIST |
| normal | norm | NORMALDISTRIBUTED |
| Poisson | pois | POISSONDISTRIBUTED |
| signed rank | signrank | SIGNTEST |
| Student’s t | t | TDIST |
| uniform | unif | UNIFORMDISTRIBUTED |
| Weibull | weibull | WEIBULL |
| Wilcoxon | wilcox | WILCOXONSIGNEDRANKTEST |
Further distributions are available in contributed packages, notably
SuppDists. Here are some examples: > ## 2-tailed p-value for t distribution
> 2*pt(-2.43, df = 13)
> ## upper 1% point for an F(2, 7) distribution
> qf(0.01, 2, 7, lower.tail = FALSE)
In Z3,there are more distributions are available:
For Example:
BERNOULLI DISTRIBUTION
BERNOULLIDISTRIBUTED(5,0.5)
Exponential Distribution
EXPONDIST(0.5,5,TRUE)
Examining the distribution of a set of data
Two slightly different summaries are given by summary and fivenum and a display of the numbers by stem (a “stem and leaf” plot). > attach(faithful)
> summary(eruptions)
Min. 1st Qu. Median Mean 3rd Qu. Max.
1.600 2.163 4.000 3.488 4.454 5.100
> fivenum(eruptions)
[1] 1.6000 2.1585 4.0000 4.4585 5.1000
> stem(eruptions)
In Z3, A stem-and-leaf diagram, also called a stem-and-leaf plot, is a diagram that quickly summarizes data while maintaining the individual data points.
STEMANDLEAFPLOT([15,16,21,23,23,26,26,30,32,41])
A stem-and-leaf plot is like a histogram, and R has a function hist to plot histograms. > hist(eruptions)
- make the bins smaller, make a plot of density
> hist(eruptions, seq(1.6, 5.2, 0.2), prob=TRUE)
> lines(density(eruptions, bw=0.1))
> rug(eruptions) # show the actual data points
Z3 will show the Histogram value along with its chart.
HISTOGRAM([1,7,12,17,20,37,50],[10,20,30,40,50],TRUE,TRUE,TRUE,TRUE)
shows the bin, frequency, cumulative and its chart.
R will show empirical cumulative distribution function by using the function ecdf.
> plot(ecdf(eruptions), do.points=FALSE, verticals=TRUE)
To fit a normal distribution and overlay the fitted CDF.
> long <- eruptions[eruptions > 3]
> plot(ecdf(long), do.points=FALSE, verticals=TRUE)
> x <- seq(3, 5.4, 0.01)
> lines(x, pnorm(x, mean=mean(long), sd=sqrt(var(long))), lty=3)
- To do in Z3.
A normal distribution shows a reasonable fit but a shorter right tail in R as
par(pty="s") # arrange for a square figure region
qqnorm(long); qqline(long)
To show the longer tail:
x <- rt(250, df = 5)
qqnorm(x); qqline(x)
- To do in Z3
To make a Q-Q plot against the generating distribution in R:
qqplot(qt(ppoints(250), df = 5), x, xlab = "Q-Q plot for t dsn")
qqline(x)
- To do in Z3
Shapiro-Wilk normality test
R Provides Shapiro-Wilk normality test:
> shapiro.test(long)
Shapiro-Wilk normality test
data: long
W = 0.9793, p-value = 0.01052
- To add in Z3
Kolmogorov-Smirnov test
R also provides One sample Kolmogorov-Smirnov test: > ks.test(long, "pnorm", mean = mean(long), sd = sqrt(var(long)))
One-sample Kolmogorov-Smirnov test
data: long
D = 0.0661, p-value = 0.4284
alternative hypothesis: two.sided
Z3 provides Kolmogorov-Smirnov test as indicated below:
KSTESTCORE(XRange,ObservedFrequency,Confidence, NewTableFlag,Test,DoMidPointOfIntervals)
This test can be modified to serve as a goodness of fit test. We can get the more detailed in [| Kolmogorov-Smirnov test]
One and two-sample tests
In R, all “classical” tests including the ones used below are in package stats which is normally loaded.
Consider the following sets of data on the latent heat of the fusion of ice (cal/gm) from Rice (1995, p.490)
Method A: 79.98 80.04 80.02 80.04 80.03 80.03 80.04 79.97 80.05 80.03 80.02 80.00 80.02
Method B: 80.02 79.94 79.98 79.97 79.97 80.03 79.95 79.97
Boxplots provide a simple graphical comparison of the two samples.
A <- scan() 79.98 80.04 80.02 80.04 80.03 80.03 80.04 79.97 80.05 80.03 80.02 80.00 80.02
B <- scan() 80.02 79.94 79.98 79.97 79.97 80.03 79.95 79.97
boxplot(A, B)
To compare the two Samples in Graphically in Z3 we can use BOXPLOT as
BOXPLOT(Array1,Array2)
T-Test
To test for the equality of the means of the two examples, we can use an unpaired t-test by
> t.test(A, B)
Welch Two Sample t-test
data: A and B t = 3.2499, df = 12.027, p-value = 0.00694
alternative hypothesis: true difference in means is not equal to 0
Z3 determines whether a samples means are distinct using Ttest.
TTESTPAIRED(Array1,Array2,HypothesizedMeanDifference,Alpha,NewTableFlag)
Here t statistic of this function calculated by using the values of average, standard deviation and a constant.
TTest paired will provide the result with the table values of Mean, Variance, Observations, Pearson Correlation, Hypothesized mean difference, Degree of Freedom, T Statistics, P(T<=t) One-Tail, T Critical One-tail, P(T<=t) Two-Tail, and T Critical Two-Tail.
Wilcoxon-Mann-Whitney Test
R supports the two sample test only assumes a common continuous distribution under the null hypothesis.
> wilcox.test(A, B)
Wilcoxon rank sum test with continuity correction
data: A and B
W = 89, p-value = 0.007497
alternative hypothesis: true location shift is not equal to 0
Z3 supports the Wilcoxon test with one tailed and Two tailed test
WILCOXONSIGNEDRANKTEST (Observations1,Observations2,ConfidenceLevel,Side,NewTableFlag)
Here when the parameter side is 1 will show the result with one tailed test.
When the parameter side is 2 then the result is for two tailed test.
There are several ways to compare graphically the two samples in R. We have already seen a pair of boxplots. The following
> plot(ecdf(A), do.points=FALSE, verticals=TRUE, xlim=range(A, B))
> plot(ecdf(B), do.points=FALSE, verticals=TRUE, add=TRUE)
In Z3,there are many ways to compare two samples. For Example:
ZTESTTWOSAMPLEFORMEANS, TTESTPAIRED and soon.
Also we can compare through Graphically: ERROR BARS,BOX PLOT
The Kolmogorov-Smirnov test is of the maximal vertical distance between the two ecdf’s, assuming a common continuous distribution:
> ks.test(A, B)
Two-sample Kolmogorov-Smirnov test
data: A and B
D = 0.5962, p-value = 0.05919
alternative hypothesis: two-sided
The Kolmogorov-Smirnov test in Z3:
KSTESTCORE (XRange,ObservedFrequency,Confidence,NewTableFlag,Test,DoMidPointOfIntervals)
Grouping, loops and conditional execution
Grouped expressions
In R, commands may be grouped together in braces, {expr_1; ...; expr_m}, in which case the value of the group is the result of the last expression in the group evaluated. Since such a group is also an expression it may, for example, be itself included in parentheses and used a part of an even larger expression, and so on.
Control statements
Conditional execution: if statements
R language has available a conditional construction of the form
> if (expr_1) expr_2 else expr_3
In Z3, the if else statement is written using '::' operator as:
(expr_1) :: {(expr_2) },
{(expr_3)};
For example,
x=34;
(x<5):: { x++ },
(x>5):: { x-- },
{
x=x*2
};
x;
In R, the “short-circuit” operators && and || are often used as part of the condition in an if
statement. Whereas & and | apply element-wise to vectors, && and || apply to vectors of
length one, and only evaluate their second argument if necessary.
In Z3, few of the following operators used are:
'==>' or '<==' as assignment operators, '@' as apply operator, ':-' as function creation operator
Repetitive execution: for loops, repeat and while
In R, there is also a for loop construction which has the form
> for (name in expr_1) expr_2
where name is the loop variable. expr 1 is a vector expression, (often a sequence like 1:20), and expr 2 is often a grouped expression with its sub-expressions written in terms of the dummy name. expr 2 is repeatedly evaluated as name ranges through the values in the vector result of expr 1.
In Z3, the same can be expressed using FOR() or FOREACH() functions:
FOR (expr_1) expr_2
or
FOR(expr_1, expr_2)
Example 1: FOR(1..2,2..4, "z=x*3*y")
The first set 1..2 behaves as the outer loop index values, and the secondary set 2..4 behaves as the inner increments, for x and y values respectively, which are associated from left to right.
Example 2: FOR 1..3 SIN
Calculates the SIN values for 1, 2 and 3.
Example 3: FOREACH(INTS(3),[SIN,COS])
Calculates SIN and COS values for 1,2 and 3.
In R,
coplot() function is used to print array of plots for respective object elements. split() function produces a list of vectors obtained by splitting a larger vector according to the classes specified by a factor. > repeat expr is a looping statement > while (condition) expr is a looping statement The break statement can be used to terminate any loop, possibly abnormally. The next statement can be used to discontinue one particular cycle and skip to the “next”.
...' to do ***'....Z3 equivalent commands to be added
Statistical models in R
This section explains about generalized linear models and nonlinear regression.
Defining statistical models; formulae
In R, The operator ~ is used to define a model formula in R. The form, for an ordinary linear model, is:
response ~ op_1 term_1 op_2 term_2 op_3 term_3 ...
where
response is a vector or matrix, (or expression evaluating to a vector or matrix) defining the response variable(s). op i is an operator, either + or -, implying the inclusion or exclusion of a term in the model, (the first is optional). term i is either • a vector or matrix expression, or 1 • a factor, or • a formula expression consisting of factors, vectors or matrices connected by formula operators.
In all cases each term defines a collection of columns either to be added to or removed from the model matrix.
For Z3, in the Statistical regression analysis,
- Y is indicated as the "Dependent variable".
- Predictor x is indicated as the "Independent Variable" .
- The output of a Regression statistics is of the form :
- Simple Regression:.
- Multiple Regression:.
In Z3, functions such as REGRESSIONANALYSIS, MULTIPLEREGRESSIONANALYSIS(), INTERCEPT(), SLOPE() etc are used.
e.g
REGRESSIONANALYSIS (YRange,XRange,ConfidenceLevel,NewTableFlag)
MULTIPLEREGRESSIONANALYSIS(yRange,xRange,ConfidenceLevel,NewTableFlag)
INTERCEPT (KnownYArray,KnownXArray)
SLOPE (KnownYArray,KnownXArray)
Refer more Z3 commands here: [| Statistical Functions]
Contrasts
...' to do ***'....to add description for R and Z3
Linear models
The basic function for fitting ordinary multiple models is lm(), and a streamlined version of the call is as follows:
> fitted.model <- lm(formula, data = data.frame)
For example
> fm2 <- lm(y ~ x1 + x2, data = production)
would fit a multiple regression model of y on x1 and x2 (with implicit intercept term).
...' to do ***'....Z3 equivalent commands to be added
Generic functions for extracting model information
In R, the value of lm() is a fitted model object; technically a list of results of class "lm". Information about the fitted model can then be displayed, extracted, plotted and so on by using generic functions that orient themselves to objects of class "lm".
These include:
add1 deviance formula predict step alias drop1 kappa print summary anova effects labels proj vcov coef family plot residuals
In Z3, inbuilt generic linear regression functions are:
ANOVA, REGRESSION, REGRESSIONANALYSIS, MULTIPLEREGRESSIONANALYSIS, LOGEST, LINEST, FORECAST, SLOPE, GROWTH etc.
Refer more Z3 statistical functions here: [| Statistical Functions]
Analysis of variance and model comparison
...' to do ***'....to add description for R and Z3
ANOVA tables
In R, a more flexible alternative to the default full ANOVA table is to compare two or more models directly using the anova() function.
> anova(fitted.model.1, fitted.model.2, ...)
The display is then an ANOVA table showing the differences between the fitted models when fitted in sequence.
Z3 has inbuilt ANOVA functions as:
ANOVASINGLEFACTOR(Array,Alpha,GroupBy,NewTableFlag)
ANOVATWOFACTORWITHOUTREPLICATION (Array,Alpha,NewTableFlag)
ANOVATWOFACTORWITHREPLICATION (Array,Alpha,NumberofSamplesPerRow,NewTableFlag)
Updating fitted models
In R, the update() function allows a model to be fitted that differs from one previously fitted usually by just a few additional or removed terms. Its form is
> new.model <- update(old.model, new.formula)
In the new.formula the special name consisting of a period, ‘.’, only, can be used to stand for “the corresponding part of the old model formula”. For example, > fm05 <- lm(y ~ x1 + x2 + x3 + x4 + x5,
>data = production) > fm6 <- update(fm05, . ~ . + x6) > smf6 <- update(fm6, sqrt(.) ~ .)
would fit a five variate multiple regression with variables (presumably) from the data frame production, fit an additional model including a sixth regressor variable, and fit a variant on the model where the response had a square root transform applied.
Other functions for exploring incremental sequences of models are add1(), drop1() and step().
...' to do ***'....to add description for Z3
Generalised linear models
In R, a generalised linear model may be described as: • There is a response, y, of interest and stimulus variables x1, x2, ..., whose values influence the distribution of the response.
• The linear predictor, and is usually written
η=β1x1 +β2x2 +···+βpxp
hence xi has no influence on the distribution of y if and only if βi = 0.
• The distribution of y is of the form
Failed to parse (syntax error): {\displaystyle fY(y;μ,φ)=exp[A\fracφ{yλ(μ)−γ(λ(μ))}+τ(y,φ)}
where φ is a scale parameter (possibly known), and is constant for all observations, A represents a prior weight, assumed known but possibly varying with the observations, and μ is the mean of y.
• The mean, μ, is a smooth invertible function of the linear predictor: μ = m(η), η = m−1(μ) = l(μ) and this inverse function, l(), is called the link function.
...' to do ***'....to add description for Z3
Families
In R, the class of generalised linear models include gaussian, binomial, poisson, inverse gaussian and gamma response distributions and also quasilikelihood models where the response distribution is not explicitly specified.
In the latter case the variance function must be specified as a function of the mean, but in other cases this function is implied by the response distribution.
Each response distribution admits a variety of link functions to connect the mean with the linear predictor. Those automatically available are shown in the following table:
Family name Link functions binomial logit, probit, log, cloglog gaussian identity, log, inverse Gamma identity, inverse, log inverse.gaussian 1/mu^2, identity, inverse, log poisson identity, log, sqrt quasi logit, probit, cloglog, identity, inverse, log, 1/mu^2, sqrt
The combination of a response distribution, a link function and various other pieces of information that are needed to carry out the modeling exercise is called the family of the generalized linear model.
In Z3, the various distribution functions include: NORMDISTRIBUTED, NORMDIST, NORMINV, LOGNORMDIST, POISSON, GAMMALN, GAMMAINV, GAMMADIST and many more.
For detailed list of inbuilt Z3 statistical functions, click here: [| Statistical Functions]
The glm() funciton
The R function to fit a generalised linear model is glm() which uses the form
> fitted.model <- glm(formula, family=family.generator, data=data.frame)
The gaussian family:
A call such as
> fm <- glm(y ~ x1 + x2, family = gaussian, data = sales)
achieves the same result as
> fm <- lm(y ~ x1+x2, data=sales)
but much less efficiently.
The binomial family:
'...to do***' Need to add description for R and Z3.
Poisson models:
In R, a Poisson generalised linear model may be fitted as in the following example:
> fmod <- glm(y ~ A + B + x, family = poisson(link=sqrt),
data = worm.counts)
'...to do***' Need to add description for Z3
Quasi-liklihood models:
For quasi-likelihood estimation and inference the precise response distribution is not specified, but rather only a link function and the form of the variance function as it depends on the mean.
Since quasi-likelihood estimation uses formally identical techniques to those for the gaussian distribution, this family provides a way of fitting gaussian models with non-standard link functions or variance functions, incidentally.
> nlfit <- glm(y ~ x1 + x2 - 1,
family = quasi(link=inverse, variance=constant),
data = biochem)
'...to do***' Need to add description for Z3
Nonlinear least squares and maximum likelihood models
R’s nonlinear optimisation routines are optim(), nlm() and nlminb(), which provide the functionality (and more) of S-Plus’s ms() and nlminb().
'...to do***' Need to add description for Z3
Least squares
'...to do***' Need to add description for R and Z3
Maximum likelihood
In R, Maximum likelihood is a method of nonlinear model fitting that applies even if the errors are not normal. The method finds the parameter values which maximize the log likelihood, or equivalently which minimize the negative log-likelihood.
This example fits a logistic model to dose-response data, which clearly could also be fit by glm(). The data are:
> x <- c(1.6907, 1.7242, 1.7552, 1.7842, 1.8113,
1.8369, 1.8610, 1.8839)
> y <- c( 6, 13, 18, 28, 52, 53, 61, 60)
> n <- c(59, 60, 62, 56, 63, 59, 62, 60)
The negative log-likelihood to minimize is:
> fn <- function(p)
sum( - (y*(p[1]+p[2]*x) - n*log(1+exp(p[1]+p[2]*x))
+ log(choose(n, y)) ))
With sensible starting values and do the fit:
> out <- nlm(fn, p = c(-50,20), hessian = TRUE)
After the fitting, out$minimum is the negative log-likelihood, and out$estimate are the maximum likelihood estimates of the parameters. To obtain the approximate SEs of the estimates:
> sqrt(diag(solve(out$hessian)))
A 95% confidence interval would be the parameter estimate ± 1.96 SE.
'...to do***' Need to add description for Z3
Some non-standard models
Some of the other facilities available in R for special regression and data analysis problems.
Mixed models:
The recommended nlme package provides functions lme() and nlme() for linear and non-linear mixed-effects models, that is linear and non-linear regressions in which some of the coefficients correspond to random effects.
Localapproximatingregressions:
The loess() function fits a non parametric regression by using a locally weighted regression. Such regressions are useful for highlighting a trend in messy data or for data reduction to give some insight into a large data set.
Robust regression:
Function lqs in the recommended package MASS provides state-of-art algorithms for highly-resistant fits. Less resistant but statistically more efficient methods are available in packages, for example function rlm in package MASS.
Additive models:
This technique aims to construct a regression function from smooth additive functions of the determining variables, usually one for each determining vari- able. Functions avas and ace in package acepack and functions bruto and mars in package mda provide some examples of these techniques in user-contributed packages to R. An extension is Generalized Additive Models, implemented in user-contributed packages gam and mgcv.
Tree-based models:
Tree-based models seek to bifurcate the data, recursively, at critical points of the determining variables in order to partition the data ultimately into groups that are as homogeneous as possible within, and as heterogeneous as possible between. The results often lead to insights that other data analysis methods tend not to yield.
Models are again specified in the ordinary linear model form. The model fitting func- tion is tree(), but many other generic functions such as plot() and text() are well adapted to displaying the results of a tree-based model fit in a graphical way. Tree models are available in R via the user-contributed packages rpart and tree.
'...to do ***' Need to add description for Z3
Graphical Procedures
Graphical facilities are an important and extremely versatile component of the R environment. R plotting commands can be used to produce a variety of graphical displays and are divided into three basic groups:
High-level
This plotting functions create a new plot on the graphics device, possibly with axes, labels, titles and so on.
Low-level
Low-level plotting functions add more information to an existing plot, such as extra points, lines and labels.
Interactive graphics
Interactive graphics functions allow you interactively add information to, or extract information from, an existing plot, using a pointing device such as a mouse.
In addition, R maintains a list of graphical parameters which can be manipulated to customize your plots.
High-level plotting commands
High-level plotting functions are designed to generate a complete plot of the data passed as arguments to the function.
Please check back in couple of days. We are updating the page.
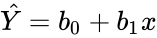 .
.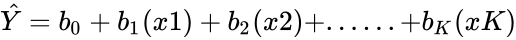 .
.