Difference between revisions of "Manuals/calci/IMLOG2"
Jump to navigation
Jump to search
| (14 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''IMLOG2( | + | <div style="font-size:30px">'''IMLOG2(Complexnumber)'''</div><br/> |
| − | *<math> | + | *<math>Complexnumber</math> is of the form <math>z=x+iy</math> |
==Description== | ==Description== | ||
*This function gives the binary logarithm of a complex number. | *This function gives the binary logarithm of a complex number. | ||
| − | *IMLOG2( | + | *<math>IMLOG2(Complexnumber)</math>, where Complexnumber is in the form of <math>z=x+iy</math>. i.e. <math>x</math> & <math>y</math> are the real numbers. |
| − | * | + | *And <math>I</math> is the imaginary unit .<math>i=\sqrt{-1}</math>. |
| − | *Binary logarithm is the inverse function of | + | *Binary logarithm is the inverse function of the Power of two functions. |
*Log base 2 is called Binary logarithm. | *Log base 2 is called Binary logarithm. | ||
*To find the Binary logarithm of a complex number we have to calculate from the natural logarithm. | *To find the Binary logarithm of a complex number we have to calculate from the natural logarithm. | ||
| − | *So log2(x+iy)=( | + | *So <math>log2(x+iy)=(log_2 e)ln(x+iy)</math>. |
| + | *We can use COMPLEX function to convert real and imaginary number in to a complex number. | ||
| + | |||
| + | ==ZOS== | ||
| + | *The syntax is to calculate Binary logarithm of a complex number is <math>IMLOG2(Complexnumber)</math>. | ||
| + | **<math>Complexnumber</math> is of the form <math>z=x+iy</math>. | ||
| + | *For e.g imlog2("2.1-3.5i") | ||
| + | {{#ev:youtube|Kd3hYo0wy4s|280|center|ImLog2}} | ||
==Examples== | ==Examples== | ||
| − | #IMLOG2("2+3i")=1.85021985921295+1.41787163085485i | + | #=IMLOG2("2+3i") = 1.85021985921295+1.41787163085485i |
| − | #IMLOG2("5-6i")=2.96536866900967-1.26388460522614i | + | #=IMLOG2("5-6i") = 2.96536866900967-1.26388460522614i |
| − | #IMLOG2("15")=3.90689059590921 | + | #=IMLOG2("15") = 3.90689059590921 |
| − | #IMLOG2("11i")=3.45943161890355+2.26618007108801i | + | #=IMLOG2("11i") = 3.45943161890355+2.26618007108801i |
| − | #IMLOG2("0")=NULL | + | #=IMLOG2("0") = NULL |
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|m-d_Xks90AM|280|center|Log of Complex Number}} | ||
==See Also== | ==See Also== | ||
*[[Manuals/calci/IMLOG10 | IMLOG10 ]] | *[[Manuals/calci/IMLOG10 | IMLOG10 ]] | ||
| − | *[[Manuals/calci/ | + | *[[Manuals/calci/LOG10 | LOG10 ]] |
*[[Manuals/calci/COMPLEX | COMPLEX ]] | *[[Manuals/calci/COMPLEX | COMPLEX ]] | ||
| − | |||
==References== | ==References== | ||
| − | [http://en.wikipedia.org/wiki/ | + | [http://en.wikipedia.org/wiki/Binary_logarithm Binary Logarithm] |
Latest revision as of 02:59, 16 March 2020
IMLOG2(Complexnumber)
- is of the form Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=x+iy}
Description
- This function gives the binary logarithm of a complex number.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle IMLOG2(Complexnumber)} , where Complexnumber is in the form of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=x+iy} . i.e. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} & Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} are the real numbers.
- And Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I} is the imaginary unit ..
- Binary logarithm is the inverse function of the Power of two functions.
- Log base 2 is called Binary logarithm.
- To find the Binary logarithm of a complex number we have to calculate from the natural logarithm.
- So Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle log2(x+iy)=(log_2 e)ln(x+iy)} .
- We can use COMPLEX function to convert real and imaginary number in to a complex number.
ZOS
- The syntax is to calculate Binary logarithm of a complex number is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle IMLOG2(Complexnumber)}
.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Complexnumber} is of the form Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=x+iy} .
- For e.g imlog2("2.1-3.5i")
Examples
- =IMLOG2("2+3i") = 1.85021985921295+1.41787163085485i
- =IMLOG2("5-6i") = 2.96536866900967-1.26388460522614i
- =IMLOG2("15") = 3.90689059590921
- =IMLOG2("11i") = 3.45943161890355+2.26618007108801i
- =IMLOG2("0") = NULL
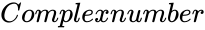 is of the form Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=x+iy}
is of the form Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=x+iy}
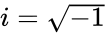 .
.