Difference between revisions of "Manuals/calci/IMLOG2"
Jump to navigation
Jump to search
| (One intermediate revision by one other user not shown) | |||
| Line 6: | Line 6: | ||
*<math>IMLOG2(Complexnumber)</math>, where Complexnumber is in the form of <math>z=x+iy</math>. i.e. <math>x</math> & <math>y</math> are the real numbers. | *<math>IMLOG2(Complexnumber)</math>, where Complexnumber is in the form of <math>z=x+iy</math>. i.e. <math>x</math> & <math>y</math> are the real numbers. | ||
*And <math>I</math> is the imaginary unit .<math>i=\sqrt{-1}</math>. | *And <math>I</math> is the imaginary unit .<math>i=\sqrt{-1}</math>. | ||
| − | *Binary logarithm is the inverse function of | + | *Binary logarithm is the inverse function of the Power of two functions. |
*Log base 2 is called Binary logarithm. | *Log base 2 is called Binary logarithm. | ||
*To find the Binary logarithm of a complex number we have to calculate from the natural logarithm. | *To find the Binary logarithm of a complex number we have to calculate from the natural logarithm. | ||
| Line 25: | Line 25: | ||
#=IMLOG2("11i") = 3.45943161890355+2.26618007108801i | #=IMLOG2("11i") = 3.45943161890355+2.26618007108801i | ||
#=IMLOG2("0") = NULL | #=IMLOG2("0") = NULL | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|m-d_Xks90AM|280|center|Log of Complex Number}} | ||
==See Also== | ==See Also== | ||
Latest revision as of 02:59, 16 March 2020
IMLOG2(Complexnumber)
- is of the form
Description
- This function gives the binary logarithm of a complex number.
- , where Complexnumber is in the form of . i.e. & are the real numbers.
- And is the imaginary unit ..
- Binary logarithm is the inverse function of the Power of two functions.
- Log base 2 is called Binary logarithm.
- To find the Binary logarithm of a complex number we have to calculate from the natural logarithm.
- So .
- We can use COMPLEX function to convert real and imaginary number in to a complex number.
ZOS
- The syntax is to calculate Binary logarithm of a complex number is .
- is of the form .
- For e.g imlog2("2.1-3.5i")
Examples
- =IMLOG2("2+3i") = 1.85021985921295+1.41787163085485i
- =IMLOG2("5-6i") = 2.96536866900967-1.26388460522614i
- =IMLOG2("15") = 3.90689059590921
- =IMLOG2("11i") = 3.45943161890355+2.26618007108801i
- =IMLOG2("0") = NULL
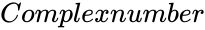 is of the form
is of the form 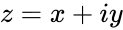
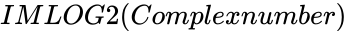 , where Complexnumber is in the form of
, where Complexnumber is in the form of  &
& 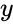 are the real numbers.
are the real numbers.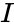 is the imaginary unit .
is the imaginary unit .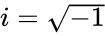 .
.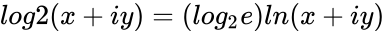 .
.