Difference between revisions of "Manuals/calci/PASCALTRIANGLE"
Jump to navigation
Jump to search
| Line 13: | Line 13: | ||
==Examples== | ==Examples== | ||
| − | *1.PASCALTRIANGLE(1)=1 | + | *1.PASCALTRIANGLE(1)= |
| − | *2.PASCALTRIANGLE(2)=1 | + | 1 |
| + | *2.PASCALTRIANGLE(2)= | ||
| + | 1 | ||
1 1 | 1 1 | ||
| − | *3.PASCALTRIANGLE(3)=1 | + | *3.PASCALTRIANGLE(3)= |
| + | 1 | ||
1 1 | 1 1 | ||
1 2 1 | 1 2 1 | ||
*4.PASCALTRIANGLE(0)=NULL | *4.PASCALTRIANGLE(0)=NULL | ||
| − | |||
==See Also== | ==See Also== | ||
Revision as of 01:50, 7 January 2014
PASCALTRIANGLE(r)
- is the row number.
Description
- This function gives the Coefficients of the Pascal triangle.
- In , r is the row number of the Pascal triangle.
- Pascal triangle is the arrangement of numbers of the Binomial coefficients in a triangular shape.
- It is started with the number 1 at the top in the 1st row.
- Then from the 2nd row each number in the triangle is the sum of the two directly above it.
- The construction is related to the binomial coefficients by Pascal's rule is :
. where is the binomial coefficient.
- This function will return the result as error when the .
Examples
- 1.PASCALTRIANGLE(1)=
1
- 2.PASCALTRIANGLE(2)=
1
1 1
- 3.PASCALTRIANGLE(3)=
1
1 1
1 2 1
- 4.PASCALTRIANGLE(0)=NULL
 is the row number.
is the row number.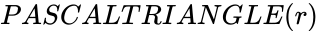 , r is the row number of the Pascal triangle.
, r is the row number of the Pascal triangle.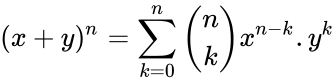 . where
. where 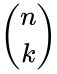 is the binomial coefficient.
is the binomial coefficient.
 .
.