Difference between revisions of "Manuals/calci/MOORE"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:30px">'''MOORE'''</div><br/>") |
|||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''MOORE'''</div><br/> | + | <div style="font-size:30px">'''MATRIX("MOORE",order)'''</div><br/> |
| + | *<math>order</math> is the size of the Moore matrix. | ||
| + | |||
| + | ==Description== | ||
| + | *This function gives the moore matrix of order 3 with the element 1. | ||
| + | *A moore matrix, is a square matrix over a finite field. | ||
| + | *When moore matrix is a square matrix, then its deteminant is called a Moore determinant. | ||
| + | *But it is unrelated to the Moore determinant of a quaternionic Hermitian matrix. | ||
| + | *The Moore matrix has successive powers of the applied to the first column, so it is an mxn matrix of the form: | ||
| + | <math>\begin{bmatrix} | ||
| + | \alpha_1 & \alpha_1^{q} &\cdots & \alpha_1^{q}^{n-1} \\ | ||
| + | \alpha_2 & \alpha_2^{q} &\cdots & \alpha_2^{q}^{n-1} \\ | ||
| + | \alpha_3 & \alpha_3^{q} &\cdots & \alpha_3^{q}^{n-1} \\ | ||
| + | \vdots & \ddots & \vdots \\ | ||
| + | \alpha_m & \alpha_m^{q} &\cdots & \alpha_m^{q}^{n-1} | ||
| + | \end{bmatrix} </math> | ||
| + | *In calci, MATRIX("moore") is giving the matrixwith the element 1 of order 3. | ||
| + | *And MATRIX("moore",4,1..4) is giving Moore matrix starting element 1 to 4 of order 4. | ||
Revision as of 09:52, 30 April 2015
MATRIX("MOORE",order)
- is the size of the Moore matrix.
Description
- This function gives the moore matrix of order 3 with the element 1.
- A moore matrix, is a square matrix over a finite field.
- When moore matrix is a square matrix, then its deteminant is called a Moore determinant.
- But it is unrelated to the Moore determinant of a quaternionic Hermitian matrix.
- The Moore matrix has successive powers of the applied to the first column, so it is an mxn matrix of the form:
Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. TeX parse error: Double exponent: use braces to clarify"): {\displaystyle {\begin{bmatrix}\alpha _{1}&\alpha _{1}^{q}&\cdots &\alpha _{1}^{q}^{n-1}\\\alpha _{2}&\alpha _{2}^{q}&\cdots &\alpha _{2}^{q}^{n-1}\\\alpha _{3}&\alpha _{3}^{q}&\cdots &\alpha _{3}^{q}^{n-1}\\\vdots &\ddots &\vdots \\\alpha _{m}&\alpha _{m}^{q}&\cdots &\alpha _{m}^{q}^{n-1}\end{bmatrix}}}
- In calci, MATRIX("moore") is giving the matrixwith the element 1 of order 3.
- And MATRIX("moore",4,1..4) is giving Moore matrix starting element 1 to 4 of order 4.
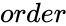 is the size of the Moore matrix.
is the size of the Moore matrix.