Difference between revisions of "Manuals/calci/TOEPLITZ"
(Created page with "<div style="font-size:30px">'''TOEPLITZ'''</div><br/>") |
|||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''TOEPLITZ'''</div><br/> | + | <div style="font-size:30px">'''MATRIX("TOEPLITZ",order)'''</div><br/> |
| + | *<math>order</math> is the size of the Toeplitz matrix. | ||
| + | |||
| + | ==Description== | ||
| + | *This function gives the matrix of order 3 with the property of toeplitz matrix. | ||
| + | *A Toeplitz matrix is a matrix with the constant values along negative sloping diagonals(descending diagonal from left to right). | ||
| + | *If the i,j element of A is denoted <math>A_{i,j}</math>, then we have | ||
| + | <math>A_{i,j} = A_{i+1,j+1} = a_{i-j}</math>. | ||
| + | *Any nxn matrix A of the form: | ||
| + | <math>\begin{bmatrix} | ||
| + | a_0 & a_{-1} & a_{-2} & \cdots & a_{-n+1} \\ | ||
| + | a_1 & a_0 & a_{-1} & \cdots \\ | ||
| + | a_2 & a_1 & \cdots \\ | ||
| + | \vdots & \ddots & \vdots \\ | ||
| + | 0 & \cdots & 0 | ||
| + | \end{bmatrix}</math> | ||
| + | <math>\begin{bmatrix} | ||
| + | a_{0} & a_{-1} & a_{-2} & \ldots & \ldots &a_{-n+1} \\ | ||
| + | a_{1} & a_0 & a_{-1} & \ddots & & \vdots \\ | ||
| + | a_{2} & a_{1} & \ddots & \ddots & \ddots& \vdots \\ | ||
| + | \vdots & \ddots & \ddots & \ddots & a_{-1} & a_{-2}\\ | ||
| + | \vdots & & \ddots & a_{1} & a_{0}& a_{-1} \\ | ||
| + | a_{n-1} & \ldots & \ldots & a_{2} & a_{1} & a_{0} | ||
| + | \end{bmatrix} </math> | ||
| + | *The property of Toeplitz matrix is :Toeplitz matrices are persymmetric. | ||
| + | *Symmetric Toeplitz matrices are both centrosymmetric and bisymmetric. | ||
| + | *Toeplitz matrices commute asymptotically. | ||
| + | |||
| + | ==Examples== | ||
| + | *MATRIX("toeplitz",15,1..10) | ||
| + | |||
| + | |||
| + | A = | ||
| + | \begin{bmatrix} | ||
| + | a_{0} & a_{-1} & a_{-2} & \ldots & \ldots &a_{-n+1} \\ | ||
| + | a_{1} & a_0 & a_{-1} & \ddots & & \vdots \\ | ||
| + | a_{2} & a_{1} & \ddots & \ddots & \ddots& \vdots \\ | ||
| + | \vdots & \ddots & \ddots & \ddots & a_{-1} & a_{-2}\\ | ||
| + | \vdots & & \ddots & a_{1} & a_{0}& a_{-1} \\ | ||
| + | a_{n-1} & \ldots & \ldots & a_{2} & a_{1} & a_{0} | ||
| + | \end{bmatrix} | ||
Revision as of 09:37, 5 May 2015
- is the size of the Toeplitz matrix.
Description
- This function gives the matrix of order 3 with the property of toeplitz matrix.
- A Toeplitz matrix is a matrix with the constant values along negative sloping diagonals(descending diagonal from left to right).
- If the i,j element of A is denoted , then we have
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_{i,j} = A_{i+1,j+1} = a_{i-j}} .
- Any nxn matrix A of the form:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{bmatrix} a_0 & a_{-1} & a_{-2} & \cdots & a_{-n+1} \\ a_1 & a_0 & a_{-1} & \cdots \\ a_2 & a_1 & \cdots \\ \vdots & \ddots & \vdots \\ 0 & \cdots & 0 \end{bmatrix}} Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{bmatrix} a_{0} & a_{-1} & a_{-2} & \ldots & \ldots &a_{-n+1} \\ a_{1} & a_0 & a_{-1} & \ddots & & \vdots \\ a_{2} & a_{1} & \ddots & \ddots & \ddots& \vdots \\ \vdots & \ddots & \ddots & \ddots & a_{-1} & a_{-2}\\ \vdots & & \ddots & a_{1} & a_{0}& a_{-1} \\ a_{n-1} & \ldots & \ldots & a_{2} & a_{1} & a_{0} \end{bmatrix} }
- The property of Toeplitz matrix is :Toeplitz matrices are persymmetric.
- Symmetric Toeplitz matrices are both centrosymmetric and bisymmetric.
- Toeplitz matrices commute asymptotically.
Examples
- MATRIX("toeplitz",15,1..10)
A =
\begin{bmatrix}
a_{0} & a_{-1} & a_{-2} & \ldots & \ldots &a_{-n+1} \\
a_{1} & a_0 & a_{-1} & \ddots & & \vdots \\
a_{2} & a_{1} & \ddots & \ddots & \ddots& \vdots \\
\vdots & \ddots & \ddots & \ddots & a_{-1} & a_{-2}\\
\vdots & & \ddots & a_{1} & a_{0}& a_{-1} \\
a_{n-1} & \ldots & \ldots & a_{2} & a_{1} & a_{0} \end{bmatrix}
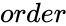 is the size of the Toeplitz matrix.
is the size of the Toeplitz matrix.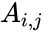 , then we have
, then we have