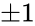Difference between revisions of "Manuals/calci/SIGNATURE"
Jump to navigation
Jump to search
| Line 9: | Line 9: | ||
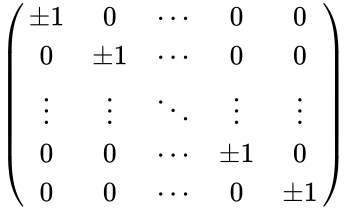
\pm 1 & 0 & \cdots & 0 & 0 \\ | \pm 1 & 0 & \cdots & 0 & 0 \\ | ||
0 & \pm 1 & \cdots & 0 & 0 \\ | 0 & \pm 1 & \cdots & 0 & 0 \\ | ||
| − | \vdots & \ddots & \vdots \\ | + | \vdots & \vdots &\ddots & \vdots & \vdots \\ |
0 & 0 & \cdots & \pm 1 & 0 \\ | 0 & 0 & \cdots & \pm 1 & 0 \\ | ||
0 & 0 & \cdots & 0 & \pm 1 | 0 & 0 & \cdots & 0 & \pm 1 | ||
Revision as of 23:47, 7 May 2015
MATRIX("SIGNATURE",order)
- is the size of the Signature matrix.
Description
- This function returns the matrix of order 3 with the property of signature matrix.
- A signature matrix is a diagonal elements are
- So signature matrix is of the form:
- Any such matrix is its own inverse, hence is an involutory matrix.
- It is consequently a square root of the identity matrix.
- Also that not all square roots of the identity are signature matrices.
- The signature matrices are both symmetric and involutory,i.e.,they are orthogonal.
- Consequently, any linear transformation corresponding to a signature matrix constitutes an isometry.
Examples
- 1. MATRIX("signature")
| 1 | 0 | 0 |
| 0 | -1 | 0 |
| 0 | 0 | 1 |
- 2.MATRIX("signature",6)
| 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | -1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | -1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 |
 is the size of the Signature matrix.
is the size of the Signature matrix.