|
|
| Line 1: |
Line 1: |
| | <div style="font-size:30px">'''REGRESSIONANALYSIS(y,x)'''</div><br/> | | <div style="font-size:30px">'''REGRESSIONANALYSIS(y,x)'''</div><br/> |
| | + | |
| | + | Regression analysis is a form of predictive modelling technique which investigates the relationship between a dependent (target) and independent variable (s) (predictor). This technique is used for forecasting, time series modelling and finding the causal effect relationship between the variables. |
| | + | |
| | + | |
| | *<math>y </math> is the set of dependent variables . | | *<math>y </math> is the set of dependent variables . |
| | *<math>x </math> is the set of independent variables. | | *<math>x </math> is the set of independent variables. |
Latest revision as of 06:02, 9 May 2016
REGRESSIONANALYSIS(y,x)
Regression analysis is a form of predictive modelling technique which investigates the relationship between a dependent (target) and independent variable (s) (predictor). This technique is used for forecasting, time series modelling and finding the causal effect relationship between the variables.
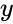 is the set of dependent variables .
is the set of dependent variables . is the set of independent variables.
is the set of independent variables.
Description
- This function is calculating the Regression analysis of the given data.
- This analysis is very useful for the analyzing the large amounts of data and making predictions.
- This analysis give the result in three table values.
- Regression statistics table.
- ANOVA table.
- Residual output.
1.Regression statistics :
- It contains multiple R, R Square, Adjusted R Square, Standard Error and observations.
- R square gives the fitness of the data with the regression line.
- That value is closer to 1 is the better the regression line fits the data.
- Standard Error refers to the estimated standard deviation of the error term. It is called the standard error of the regression.
2.ANOVA table:
- ANOVA is the analysis of variance.
- This table splits in to two components which is Residual and Regression.
Total sum of squares = Residual (error) sum of squares + Regression (explained) sum of squares.
- Also this table gives the probability, T stat, significance of F and P.
- When the significance of F is < 0.05, then the result for the given data is statistically significant.
- When the significance of F is > 0.05, then better to stop using this set of independent variables.
- Then remove a variable with a high P-value and return the regression until Significance F drops below 0.05.
- So the Significance of P value should be <0.05.
- This table containing the regression coefficient values also.
3.Residual output:
- The residuals show you how far away the actual data points are from the predicted data points.
Examples
1.
Spreadsheet
|
A |
B
|
| 1
|
Temperature |
Drying Time(Hrs)
|
| 2
|
54 |
8
|
| 3
|
63 |
6
|
| 4
|
75 |
3
|
| 5
|
82 |
1
|
=REGRESSIONANALYSIS(A2:A5,B2:B5)
REGRESSION ANALYSIS OUTPUT
Summary Output
| Regression Statistics |
|
| Multiple R |
-0.9989241524588298
|
| R Square |
0.9978494623655915
|
| v14193 |
0.9967741935483871
|
| v15308 |
0.7071067811865362
|
ANOVA
| Source of Variation |
Sum Of Squares |
Degree Of Freedom |
Mean Of Squares |
F |
Significance F
|
| Regression:
|
464 |
1 |
464 |
928 |
0.0010758475411702228
|
| Residual:
|
1 |
2 |
0.5 |
|
|
| Total:
|
465 |
3 |
|
|
|
ANOVA
|
Coefficients |
Standard Error |
T Statistics |
Probability |
Lower 95% |
Upper 95%
|
| Intercept:
|
86.5 |
0.6885767430246738 |
125.62143708199632 |
0.00006336233990811291 |
83.53729339698289 |
89.46270660301711
|
| X Variable
|
-4 |
0.13130643285972046 |
-30.463092423456118 |
0.0010758475411701829 |
-4.564965981777541 |
-3.435034018222459
|
Residual Output
| Observation |
Predicted Y |
Residuals |
Standard Residuals
|
| 1 |
54.5 |
-0.5 |
-0.8660254037844387
|
| 2 |
62.5 |
0.5 |
0.8660254037844387
|
| 3 |
74.5 |
0.5 |
0.8660254037844387
|
| 4 |
82.5 |
-0.5 |
-0.8660254037844387
|
2.
Spreadsheet
|
A |
B |
C
|
| 1
|
Unit sales |
Ads |
population
|
| 2
|
4000 |
12000 |
300000
|
| 3
|
5200 |
13150 |
411000
|
| 4
|
6800 |
14090 |
500000
|
| 5
|
8000 |
11900 |
650000
|
| 6
|
10000 |
15000 |
800000
|
- REGRESSIONANALYSIS(A2:A6,B2:C6)
REGRESSION ANALYSIS OUTPUT
SUMMARY OUTPUT
| Regression Statistics |
|
| Multiple R
|
0.9973790019059987
|
| R Square
|
0.9947648734430062
|
| Adjusted R Square
|
0.9895297468860125
|
| Standard Error
|
240.4075647503864
|
| Observations
|
5
|
ANOVA
|
df |
SS |
MS |
F |
Significance F
|
| Regression:
|
2 |
21964408.405621577 |
10982204.202810789 |
190.0173496501376 |
0.00523512655699377
|
| Residual:
|
2 |
115591.59437842245 |
57795.797189211225 |
|
|
| Total:
|
4 |
22080000 |
|
|
|
|
Coefficients |
Standard Error |
t Stat |
P-value |
Lower 95% |
Upper 95% |
Lower 95.0% |
Upper 95.0%
|
| Intercept:
|
-1096.09242 |
1259.21057 |
-0.87046 |
0.47583 |
-6514.03824 |
4321.85339 |
-6514.03824 |
4321.8533
|
| X Variable1
|
0.14076 |
0.10798 |
1.30359 |
0.32223 |
-0.32384 |
0.60538 |
-0.32384 |
0.60538
|
| X Variable2
|
0.01133 |
0.00073 |
15.45951 |
0.00415 |
0.00818 |
0.01449 |
0.00818 |
0.01449
|
Residual Output
| Observation |
Predicted Y |
Residuals |
Standard Residuals
|
| 1 |
593.1069112686723 |
3406.8930887313277 |
1.5209125615152896
|
| 2 |
754.9885142857306 |
4445.011485714269 |
1.9843516155712606
|
| 3 |
887.3091289257611 |
5912.690871074239 |
2.6395562126436793
|
| 4 |
579.0302501367541 |
7420.969749863246 |
3.312885323147887
|
| 5 |
1015.4067452262161 |
8984.593254773783 |
4.010921501026477
|
Related Videos
See Also
References
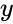 is the set of dependent variables .
is the set of dependent variables . is the set of independent variables.
is the set of independent variables.