Difference between revisions of "Manuals/calci/HARMONICSERIES"
Jump to navigation
Jump to search
(Created page with "==HAR") |
|||
| Line 1: | Line 1: | ||
| − | == | + | <div style="font-size:30px">'''HARMONICSERIES (Start,Numbers,OnlyNth)'''</div><br/> |
| + | *<math>Start</math> are any positive integer . | ||
| + | *<math>Numbers</math> is the number of the series. | ||
| + | *<math>OnlyNth </math> is the Nth term of the series. | ||
| + | |||
| + | ==Description== | ||
| + | *This sfunction displays the Harmonic series of the numbers. | ||
| + | *A series is an expression with an infinite number of terms, like this:\sum_{n=1}^{/infty} \frac{1}{n} = 1+ \frac{1}{2}+\frac{1}{3}+\frac{1}{4}+.... | ||
| + | *This is the divergent infinite series. | ||
| + | *In HARMONICSERIES(Start,Numbers,OnlyNth),Start is the beginning number of the series, Numbers is number of the number in the series and OnlyNth is the nth term of the Harmonic Series. | ||
| + | *Every term of the series after the first is the harmonic mean of the neighboring terms. | ||
| + | *The phrase harmonic mean likewise derives from music. | ||
Revision as of 14:35, 28 November 2016
HARMONICSERIES (Start,Numbers,OnlyNth)
- are any positive integer .
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Numbers} is the number of the series.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle OnlyNth } is the Nth term of the series.
Description
- This sfunction displays the Harmonic series of the numbers.
- A series is an expression with an infinite number of terms, like this:\sum_{n=1}^{/infty} \frac{1}{n} = 1+ \frac{1}{2}+\frac{1}{3}+\frac{1}{4}+....
- This is the divergent infinite series.
- In HARMONICSERIES(Start,Numbers,OnlyNth),Start is the beginning number of the series, Numbers is number of the number in the series and OnlyNth is the nth term of the Harmonic Series.
- Every term of the series after the first is the harmonic mean of the neighboring terms.
- The phrase harmonic mean likewise derives from music.
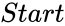 are any positive integer .
are any positive integer .