Difference between revisions of "Manuals/calci/IMLOG2"
Jump to navigation
Jump to search
(Created page with "<div id="16SpaceContent" align="left"><div class="ZEditBox" align="justify"> Syntax </div></div> ---- <div id="4SpaceContent" align="left"><div class="ZEditBox" align=...") |
|||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''IMLOG2(z)'''</div><br/> |
| + | *<math>z</math> is the complex number is of the form <math>x+iy</math> | ||
| − | + | ==Description== | |
| + | *This function gives the binary logarithm of a complex number. | ||
| + | *IMLOG2(z),Where z is the complex number in the form of "x+iy".i.e. x&y are the real numbers. | ||
| + | *'I' imaginary unit .i=sqrt(-1). | ||
| + | *Binary logarithm is the inverse function of n ↦ 2n. | ||
| + | *Log base 2 is called Binary logarithm. | ||
| + | *To find the Binary logarithm of a complex number we have to calculate from the natural logarithm. | ||
| + | *So log2(x+iy)=(log2 e)ln(x+iy).We can use COMPLEX function to convert real and imaginary number in to a complex number. | ||
| − | + | ==Examples== | |
| − | |||
| − | |||
| − | + | #IMLOG2("2+3i")=1.85021985921295+1.41787163085485i | |
| + | #IMLOG2("5-6i")=2.96536866900967-1.26388460522614i | ||
| + | #IMLOG2("15")=3.90689059590921 | ||
| + | #IMLOG2("11i")=3.45943161890355+2.26618007108801i | ||
| + | #IMLOG2("0")=NULL | ||
| − | + | ==See Also== | |
| − | + | *[[Manuals/calci/IMLOG10 | IMLOG10 ]] | |
| − | + | *[[Manuals/calci/LOG2 | LOG2 ]] | |
| + | *[[Manuals/calci/COMPLEX | COMPLEX ]] | ||
| − | |||
| − | + | ==References== | |
| − | + | [http://en.wikipedia.org/wiki/Bessel_function Bessel Function] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Revision as of 03:13, 16 December 2013
IMLOG2(z)
- is the complex number is of the form
Description
- This function gives the binary logarithm of a complex number.
- IMLOG2(z),Where z is the complex number in the form of "x+iy".i.e. x&y are the real numbers.
- 'I' imaginary unit .i=sqrt(-1).
- Binary logarithm is the inverse function of n ↦ 2n.
- Log base 2 is called Binary logarithm.
- To find the Binary logarithm of a complex number we have to calculate from the natural logarithm.
- So log2(x+iy)=(log2 e)ln(x+iy).We can use COMPLEX function to convert real and imaginary number in to a complex number.
Examples
- IMLOG2("2+3i")=1.85021985921295+1.41787163085485i
- IMLOG2("5-6i")=2.96536866900967-1.26388460522614i
- IMLOG2("15")=3.90689059590921
- IMLOG2("11i")=3.45943161890355+2.26618007108801i
- IMLOG2("0")=NULL
See Also
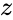 is the complex number is of the form
is the complex number is of the form