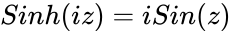Difference between revisions of "Manuals/calci/SINH"
Jump to navigation
Jump to search
| Line 6: | Line 6: | ||
*Also it is called as Circular function. | *Also it is called as Circular function. | ||
* Here <math>SINH=\frac{e^z-e^{-z}}{2}</math> or <math>-iSIN(iz)</math>, where <math>i</math> is the imginary unit and <math>i=\sqrt{-1}</math> | * Here <math>SINH=\frac{e^z-e^{-z}}{2}</math> or <math>-iSIN(iz)</math>, where <math>i</math> is the imginary unit and <math>i=\sqrt{-1}</math> | ||
| − | *Also relation between | + | *Also relation between Hyperbolic & Trigonometric function is <math>Sin(iz)=iSin(hz)</math> & <math>Sinh(iz)= iSin(z)</math> |
| − | *SINH(- | + | *SINH(-z)=-SINH(z) |
== Examples == | == Examples == | ||
Revision as of 22:40, 4 November 2013
SINH(z)
- where z is any real number
Description
- This function gives the hyperbolic sin of 'z'.
- Also it is called as Circular function.
- Here or , where is the imginary unit and
- Also relation between Hyperbolic & Trigonometric function is &
- SINH(-z)=-SINH(z)
Examples
SINH(z)
- z is any real number.
| SINH(z) | Value(Radian) |
| SINH(0) | 0 |
| SINH(10) | 11013.23287 |
| SINH(-3) | -10.0178749274099 |
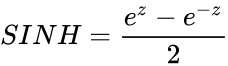 or
or 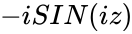 , where
, where  is the imginary unit and
is the imginary unit and 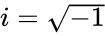
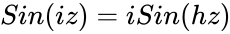 &
&