Difference between revisions of "Manuals/calci/COTH"
Jump to navigation
Jump to search
| Line 3: | Line 3: | ||
==Description== | ==Description== | ||
| − | *This function gives the hyperbolic | + | *This function gives the hyperbolic Cotangent of 'z'. |
| + | *It's also called as Circular function. | ||
*COTH is the reciprocal of TANH function. | *COTH is the reciprocal of TANH function. | ||
| − | *COTH | + | *<math>COTH(z)=\frac{Cosh(z)}{Sinh(z)}</math> i.e.<math>\frac( e^z+e^{-z}} {e^z-e^{-z}}</math> or Icot(iz).where 'I' is the imginary unit and i=sqrt(-1). |
*Also relation between hyperbolic &trignometric function is | *Also relation between hyperbolic &trignometric function is | ||
*cot(iz)=-icothz&coth(iz)=-icot z | *cot(iz)=-icothz&coth(iz)=-icot z | ||
Revision as of 06:22, 5 November 2013
COTH(z)
- where z is any real number
Description
- This function gives the hyperbolic Cotangent of 'z'.
- It's also called as Circular function.
- COTH is the reciprocal of TANH function.
- i.e.Failed to parse (syntax error): {\displaystyle \frac( e^z+e^{-z}} {e^z-e^{-z}}} or Icot(iz).where 'I' is the imginary unit and i=sqrt(-1).
- Also relation between hyperbolic &trignometric function is
- cot(iz)=-icothz&coth(iz)=-icot z
Examples
COTH(z)
- z is any real number.
| COTH(z) | Value(Radian) |
| COTH(1) | 1.3130352854993312 |
| COTH(30) | 1 |
| COTH(-45) | -1 |
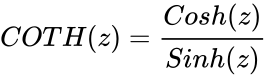 i.e.Failed to parse (syntax error): {\displaystyle \frac( e^z+e^{-z}} {e^z-e^{-z}}}
or Icot(iz).where 'I' is the imginary unit and i=sqrt(-1).
i.e.Failed to parse (syntax error): {\displaystyle \frac( e^z+e^{-z}} {e^z-e^{-z}}}
or Icot(iz).where 'I' is the imginary unit and i=sqrt(-1).