Difference between revisions of "Manuals/calci/CSCH"
Jump to navigation
Jump to search
| Line 6: | Line 6: | ||
*This function gives the Hyperbolic Cosecant of 'z'. | *This function gives the Hyperbolic Cosecant of 'z'. | ||
*It's also called as Circular function. | *It's also called as Circular function. | ||
| − | *Here <math>CSCH= (sinh(z))^{-1}</math> ie, <math>\frac{2}{e^z-e^{-z}}</math> or <math>icsc(iz)</math>, where <math>i</math> is the imaginary unit and <math>i=\sqrt{-1}</math> | + | *Here <math>CSCH(z)= (sinh(z))^{-1}</math> ie, <math>\frac{2}{e^z-e^{-z}}</math> or <math>icsc(iz)</math>, where <math>i</math> is the imaginary unit and <math>i=\sqrt{-1}</math> |
*The relation between Hyperbolic & Trigonometric function is <math>Csc(iz) = -iCsch(z)</math> & <math>Csch(iz)=-iCsc(z)</math> | *The relation between Hyperbolic & Trigonometric function is <math>Csc(iz) = -iCsch(z)</math> & <math>Csch(iz)=-iCsc(z)</math> | ||
*CSCH(-z)=-CSCH(z) | *CSCH(-z)=-CSCH(z) | ||
Revision as of 00:30, 7 November 2013
CSCH(z)
- Where z is any real number
- It is read as COSECH(z)
Description
- This function gives the Hyperbolic Cosecant of 'z'.
- It's also called as Circular function.
- Here Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle CSCH(z)= (sinh(z))^{-1}} ie, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{e^z-e^{-z}}} or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle icsc(iz)} , where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} is the imaginary unit and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i=\sqrt{-1}}
- The relation between Hyperbolic & Trigonometric function is & Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Csch(iz)=-iCsc(z)}
- CSCH(-z)=-CSCH(z)
Examples
CSCH(z)
- z is any real number.
| CSCH(z) | Value(Radian) |
| CSCH(0) | Infinity |
| CSCH(7) | 0.00182376 |
| CSCH(-2) | 0.27572056 |
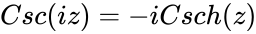 & Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Csch(iz)=-iCsc(z)}
& Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Csch(iz)=-iCsc(z)}