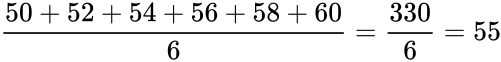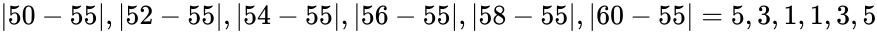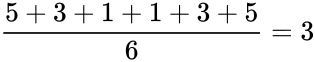Difference between revisions of "Manuals/calci/AVEDEV"
Jump to navigation
Jump to search
| Line 10: | Line 10: | ||
#To find the deviation of each value, subtract all numbers with its mean value. | #To find the deviation of each value, subtract all numbers with its mean value. | ||
#Then find the average deviation, add all the deviation values and divide by the total number of given numbers. | #Then find the average deviation, add all the deviation values and divide by the total number of given numbers. | ||
| − | + | :<math>Average Deviation =\sum_{i=1}^{n} \frac{xi-\bar{x}}{n}</math> | |
| − | <math>Average Deviation =\sum_{i=1}^{n} \frac{xi-\bar{x}}{n}</math> | ||
*Here <math>xi</math> is the observation. | *Here <math>xi</math> is the observation. | ||
*<math>\bar{x}</math> is the mean. | *<math>\bar{x}</math> is the mean. | ||
Revision as of 00:32, 26 November 2013
AVEDEV(n1,n2,n3...)
- are any real numbers.
Description
- AVEDEV returns the average of the absolute deviations of data points from their mean.
- Arguments can be numbers,names,arrays or references.
This function gives the average absolute deviation of a given set of numbers. The Average deviation is calculated in three steps:
- We have to find the mean .
- To find the deviation of each value, subtract all numbers with its mean value.
- Then find the average deviation, add all the deviation values and divide by the total number of given numbers.
- Here is the observation.
- is the mean.
- is the number of given set of observations.
Here we have to give more than one arguments. Arguments can be either number, name,logical values, arrays or cell references that contain numbers.
This function will give the result as error, when the text couldn't convert in to numbers.
Examples
- =AVEDEV(50,52, 54, 56, 58, 60) gives the result 3
Steps
- Mean =
- Deviation =
- Average Deviation =
- =AVEDEV(-20,40,-30,50,60) = 36
- =AVEDEV(-1.2,3.5,7,2,8.3,9.1) = 3.35
- =AVEDEV(B2:B5) = 1.75
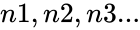 are any real numbers.
are any real numbers.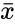 .
.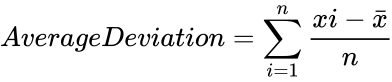
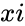 is the observation.
is the observation. is the number of given set of observations.
is the number of given set of observations.