Difference between revisions of "Manuals/calci/EXPONDIST"
| Line 9: | Line 9: | ||
*This describes the time between events in a Poisson process i.e, a process in which events occur continuously and independently at a constant average rate. | *This describes the time between events in a Poisson process i.e, a process in which events occur continuously and independently at a constant average rate. | ||
*For e.g Time between successive vehicles arrivals at a workshop. | *For e.g Time between successive vehicles arrivals at a workshop. | ||
| − | *In <math>EXPONDIST(x, | + | *In <math>EXPONDIST(x,lambda,cu)</math>, <math>x</math> is the value of the function, <math> lambda</math> is called rate parameter and <math>cu</math>(cumulative) is the TRUE or FALSE. |
*This function will give the Cumulative Distribution Function when <math>cu</math> is TRUE, otherwise it will give the Probability Density Function , when <math>cu</math> is FALSE. | *This function will give the Cumulative Distribution Function when <math>cu</math> is TRUE, otherwise it will give the Probability Density Function , when <math>cu</math> is FALSE. | ||
*Suppose we are not giving the <math>cu</math> value, by default it will consider the <math>cu</math> value is FALSE. | *Suppose we are not giving the <math>cu</math> value, by default it will consider the <math>cu</math> value is FALSE. | ||
Revision as of 02:57, 5 December 2013
- is the value of the function
- is the value of the rate parameter
- is the logical value like TRUE or FALSE
Description
- This function gives the Exponential Distribution. This distribution is used to model the time until something happens in the process.
- This describes the time between events in a Poisson process i.e, a process in which events occur continuously and independently at a constant average rate.
- For e.g Time between successive vehicles arrivals at a workshop.
- In , is the value of the function, is called rate parameter and (cumulative) is the TRUE or FALSE.
- This function will give the Cumulative Distribution Function when is TRUE, otherwise it will give the Probability Density Function , when is FALSE.
- Suppose we are not giving the value, by default it will consider the value is FALSE.
- This function will give the error result when
1. or is non-numeric. 2. or
The Probability Density Function of an Exponential Distribution is
or
- where is the rate parameter and is the Heaviside step function
- This function is valid only on the interval [0,infinity].
The Cumulative Distribution Function is : Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(x;\lambda)=1-e^{-\lambda x}, x \ge 0}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0 , x<0 }
or
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(x,\lambda)=1-e^{-\lambda x}.H(x)}
- The mean or expected value of the Exponential Distribution is: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E[x]=\frac{1}{\lambda}}
- The variance of the Exponential Distribution is: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Var[x]=\frac{1}{\lambda^2}} .
Examples
Question : If jobs arrive at an average of 15 seconds, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda =5} per minute, what is the probability of waiting 30 seconds, i.e 0.5 min? Here Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda =5} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=0.5}
- =EXPONDIST(0.5,5,TRUE) = 0.917915001
- =EXPONDIST(5,3,TRUE) = 0.999999694
- =EXPONDIST(0.4,2,FALSE) = 0.898657928"
 is the value of the function
is the value of the function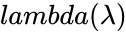 is the value of the rate parameter
is the value of the rate parameter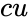 is the logical value like TRUE or FALSE
is the logical value like TRUE or FALSE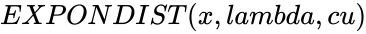 ,
, 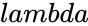 is called rate parameter and
is called rate parameter and 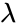 is non-numeric.
2.
is non-numeric.
2. 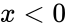 or
or 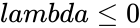
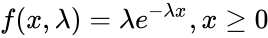
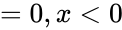
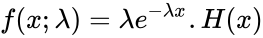
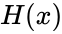 is the Heaviside step function
is the Heaviside step function