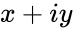Difference between revisions of "Manuals/calci/IMLOG2"
Jump to navigation
Jump to search
| Line 4: | Line 4: | ||
==Description== | ==Description== | ||
*This function gives the binary logarithm of a complex number. | *This function gives the binary logarithm of a complex number. | ||
| − | *IMLOG2(z), | + | *<math>IMLOG2(z), where z is the complex number in the form of <math>x+iy<math>. i.e. <math>x<math> & <math>y<math> are the real numbers. |
| − | * | + | *<math>I<math> imaginary unit .<math>i=\sqrt{-1}<math>. |
| − | *Binary logarithm is the inverse function of n ↦ 2n. | + | *Binary logarithm is the inverse function of <math>n ↦ 2n<math>. |
*Log base 2 is called Binary logarithm. | *Log base 2 is called Binary logarithm. | ||
*To find the Binary logarithm of a complex number we have to calculate from the natural logarithm. | *To find the Binary logarithm of a complex number we have to calculate from the natural logarithm. | ||
| − | *So log2(x+iy)=( | + | *So <math>log2(x+iy)=(log_2 e)ln(x+iy)</math>. |
*We can use COMPLEX function to convert real and imaginary number in to a complex number. | *We can use COMPLEX function to convert real and imaginary number in to a complex number. | ||
Revision as of 05:33, 16 December 2013
IMLOG2(z)
- is the complex number is of the form
Description
- This function gives the binary logarithm of a complex number.
- Failed to parse (syntax error): {\displaystyle IMLOG2(z), where z is the complex number in the form of <math>x+iy<math>. i.e. <math>x<math> & <math>y<math> are the real numbers. *<math>I<math> imaginary unit .<math>i=\sqrt{-1}<math>. *Binary logarithm is the inverse function of <math>n ↦ 2n<math>. *Log base 2 is called Binary logarithm. *To find the Binary logarithm of a complex number we have to calculate from the natural logarithm. *So <math>log2(x+iy)=(log_2 e)ln(x+iy)} .
- We can use COMPLEX function to convert real and imaginary number in to a complex number.
Examples
- IMLOG2("2+3i")=1.85021985921295+1.41787163085485i
- IMLOG2("5-6i")=2.96536866900967-1.26388460522614i
- IMLOG2("15")=3.90689059590921
- IMLOG2("11i")=3.45943161890355+2.26618007108801i
- IMLOG2("0")=NULL
- Imln("8") for that it should consider the imaginary value is zero,but calci is not considering like EXCEL
See Also
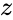 is the complex number is of the form
is the complex number is of the form