Difference between revisions of "Manuals/calci/IMLOG10"
Jump to navigation
Jump to search
| Line 5: | Line 5: | ||
*This function gives the common logarithm of a complex number. | *This function gives the common logarithm of a complex number. | ||
*IMLOG10(z), where <math>z</math> is the complex number in the form of <math>x+iy</math>. i.e <math>x</math> & <math>y</math> are the real numbers. | *IMLOG10(z), where <math>z</math> is the complex number in the form of <math>x+iy</math>. i.e <math>x</math> & <math>y</math> are the real numbers. | ||
| − | *<math>I</math> is the imaginary unit .<math>i=sqrt{-1}</math>. | + | *<math>I</math> is the imaginary unit .<math>i=\sqrt{-1}</math>. |
*Log base 10, is known as the common Logarithm or Decadic logarithm, is the logarithm to the base 10. | *Log base 10, is known as the common Logarithm or Decadic logarithm, is the logarithm to the base 10. | ||
*To find the common logarithm of a complex number, we have to calculate from the Natural Logarithm. | *To find the common logarithm of a complex number, we have to calculate from the Natural Logarithm. | ||
| − | *So <math>log10(x+iy)=( | + | *So <math>log10(x+iy)=(log_{10} e)ln(x+iy)</math>. |
*We can use COMPLEX function to convert real and imaginary number into a complex number. | *We can use COMPLEX function to convert real and imaginary number into a complex number. | ||
Revision as of 23:29, 17 December 2013
IMLOG10(z)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} is the complex number is of the form Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x+iy}
Description
- This function gives the common logarithm of a complex number.
- IMLOG10(z), where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} is the complex number in the form of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x+iy} . i.e Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} & Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} are the real numbers.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I} is the imaginary unit .Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i=\sqrt{-1}} .
- Log base 10, is known as the common Logarithm or Decadic logarithm, is the logarithm to the base 10.
- To find the common logarithm of a complex number, we have to calculate from the Natural Logarithm.
- So .
- We can use COMPLEX function to convert real and imaginary number into a complex number.
Examples
- =IMLOG10("6+7i")=0.964709462857146+0.37443569720420i
- =IMLOG10("4-5i")=0.806391928359868-0.389151908999031i
- =IMLOG10("8")=0.903089986991944
- =IMLOG10("3i")=0.477121254719662+0.682188176920921i
- =IMLOG10("0")=NULL
- Imln("8") for that it should consider the imaginary value is zero.
See Also
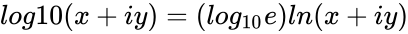 .
.