Difference between revisions of "Manuals/calci/IRR"
Jump to navigation
Jump to search
| Line 24: | Line 24: | ||
|+1..10@SQRT | |+1..10@SQRT | ||
|- | |- | ||
| − | ! !! A !! B | + | ! !! A !! B |
| − | |||
|- | |- | ||
| − | | -100000 || -500000 | + | ! 1 |
| − | + | | -100000 || -500000 | |
|- | |- | ||
| + | ! 2 | ||
| 10000 || 32000 | | 10000 || 32000 | ||
| + | |- | ||
! 3 | ! 3 | ||
| + | |28000 || 45000 | ||
|- | |- | ||
| − | |||
! 4 | ! 4 | ||
| + | |20000 || 100000 | ||
|- | |- | ||
| − | |||
! 5 | ! 5 | ||
| + | | 32500 || 150000 | ||
|- | |- | ||
| − | |||
! 6 | ! 6 | ||
| + | | 59000 || 275000 | ||
|- | |- | ||
| − | + | ! 7 | |
| − | ! 7 | ||
| − | |||
|1000 ||67000 | |1000 ||67000 | ||
|} | |} | ||
| Line 52: | Line 52: | ||
#=IRR(B1:B7) = 6.7% | #=IRR(B1:B7) = 6.7% | ||
#=IRR(B1:B5,5%)= -160.99% | #=IRR(B1:B5,5%)= -160.99% | ||
| − | |||
==See Also== | ==See Also== | ||
Revision as of 00:39, 31 March 2014
IRR(v,g)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v} is the array of values.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g} is the number is close to the result of IRR.
Description
- This function gives the internal rate of return of a cash flow stream associated with an investment.
- The Internal Rate of Return is the interest rate that makes the Net Present Value zero.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle IRR} is similar to the net present value calculation.
- In Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle IRR(v,g)} , is an values which is the array or a reference to cells that contain numbers for which you want to calculate the internal rate of return.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g} is the guess which is indicating the number that you guess is close to the result of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle IRR} .
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v} must have atleast one positive and one negative value to find the internal rate of return.
- The value of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v} can be array or reference argument contains text, logical values or empty cells, the values which are ignored.
- The Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g} value is optional, when we are omitting the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g} value,by default it will consider the value as 10%(0.1).
- The calculation of uses an iterative method.
- The value is starting from g value and doing the calculation until the result is accurate within 0.00001%.
- Also Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle IRR} can't find the result that works after 20 tries.
- The calculating Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle IRR} for cash flows occurring at any other regular intervals like quarterly or semi annual by using respective factor.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle IRR} is also called effective interest rate, or rate of return.
- It is used to evaluate an investment or project.
- The function will return the result as error after the 20 tries in the iterative method.
Examples
| A | B | |
|---|---|---|
| 1 | -100000 | -500000 |
| 2 | 10000 | 32000 |
| 3 | 28000 | 45000 |
| 4 | 20000 | 100000 |
| 5 | 32500 | 150000 |
| 6 | 59000 | 275000 |
| 7 | 1000 | 67000 |
- =IRR(A1:A6)=11.88%
- =IRR(A1:A5,20%) = -3.45%
- =IRR(B1:B7) = 6.7%
- =IRR(B1:B5,5%)= -160.99%
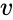 is an values which is the array or a reference to cells that contain numbers for which you want to calculate the internal rate of return.
is an values which is the array or a reference to cells that contain numbers for which you want to calculate the internal rate of return. uses an iterative method.
uses an iterative method.