Difference between revisions of "Manuals/calci/EXPONDIST"
| Line 8: | Line 8: | ||
*This describes the time between events in a Poisson process i.e, a process in which events occur continuously and independently at a constant average rate. | *This describes the time between events in a Poisson process i.e, a process in which events occur continuously and independently at a constant average rate. | ||
*For e.g Time between successive vehicles arrivals at a workshop. | *For e.g Time between successive vehicles arrivals at a workshop. | ||
| + | *Exponential distribution is the only continuous memoryless random distribution. It is a continuous analog of the Geometric distribution. | ||
*In <math>EXPONDIST(x,lambda,cumulative)</math>, <math>x</math> is the value of the function, <math> lambda</math> is called rate parameter and <math>cumulative</math> is either TRUE or FALSE. | *In <math>EXPONDIST(x,lambda,cumulative)</math>, <math>x</math> is the value of the function, <math> lambda</math> is called rate parameter and <math>cumulative</math> is either TRUE or FALSE. | ||
*This function will give the Cumulative Distribution Function when <math>cumulative</math> is TRUE, otherwise it will give the Probability Density Function , when <math>cumulative</math> is FALSE. | *This function will give the Cumulative Distribution Function when <math>cumulative</math> is TRUE, otherwise it will give the Probability Density Function , when <math>cumulative</math> is FALSE. | ||
Revision as of 23:20, 8 June 2014
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} is the value of the function
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle lambda(\lambda)} is the value of the rate parameter
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle cumulative} is the logical value like TRUE or FALSE
Description
- This function gives the Exponential Distribution. This distribution is used to model the time until something happens in the process.
- This describes the time between events in a Poisson process i.e, a process in which events occur continuously and independently at a constant average rate.
- For e.g Time between successive vehicles arrivals at a workshop.
- Exponential distribution is the only continuous memoryless random distribution. It is a continuous analog of the Geometric distribution.
- In Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle EXPONDIST(x,lambda,cumulative)} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} is the value of the function, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle lambda} is called rate parameter and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle cumulative} is either TRUE or FALSE.
- This function will give the Cumulative Distribution Function when Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle cumulative} is TRUE, otherwise it will give the Probability Density Function , when Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle cumulative} is FALSE.
- Suppose we are not giving the value, by default it will consider the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle cumulative} value is FALSE.
- This function will give the error result when
1. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x}
or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle lambda}
is non-numeric.
2. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x<0}
or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle lambda \le 0}
The Probability Density Function of an Exponential Distribution is: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x,\lambda)=\begin{cases} \lambda e^{-\lambda x} &, x \ge 0 \\ 0 &, x<0 \end{cases}} or
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x;\lambda)= \lambda e^{-\lambda x} .H(x)}
- where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda} is the rate parameter and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H(x)} is the Heaviside step function
- This function is valid only on the interval [0,infinity].
The Cumulative Distribution Function is : Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(x,\lambda)=\begin{cases} 1-e^{-\lambda x} &, x \ge 0 \\ 0 &, x<0 \end{cases}} or
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(x,\lambda)=1-e^{-\lambda x}.H(x)}
Examples
Question : If jobs arrive at an average of 15 seconds, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda =5} per minute, what is the probability of waiting 30 seconds, i.e 0.5 min? Here Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda =5} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=0.5}
- =EXPONDIST(0.5,5,TRUE) = 0.917915001
- =EXPONDIST(5,3,TRUE) = 0.999999694
- =EXPONDIST(0.4,2,FALSE) = 0.898657928"
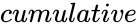 value, by default it will consider the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle cumulative}
value is FALSE.
value, by default it will consider the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle cumulative}
value is FALSE.