Difference between revisions of "Manuals/calci/CHIINV"

From ZCubes Wiki
Jump to navigation Jump to search
Line 1: Line 1:
−
<div style="font-size:30px">'''CHIINV(prob,df)'''</div><br/>
+
<div style="font-size:30px">'''CHIINV(probability,degreesoffreedom)'''</div><br/>
−
*Where <math>prob</math> is the probability value associated with the Chi-squared Distribution
+
*Where <math>probability</math> is the value associated with the Chi-squared Distribution
−
*<math>df</math> is the number of Degrees of Freedom
+
*<math>degreesoffreedom</math> is the number of Degrees of Freedom
  
 
==Description==
 
==Description==
Line 17: Line 17:
 
  3.<math> df < 1 </math>or <math>df>10^{10}</math>
 
  3.<math> df < 1 </math>or <math>df>10^{10}</math>
 
  4.Also <math> prob < 0 </math> or <math>prob>1</math>.
 
  4.Also <math> prob < 0 </math> or <math>prob>1</math>.
 +
 +
==ZOS Section==
 +
*The syntax is to calculate CHIINV in ZOS is <math>CHIINV(probability,degreesoffreedom)</math>.
 +
**Where <math>probability</math> is the  value associated with the Chi-squared Distribution
 +
**<math>degreesoffreedom</math> is the number of Degrees of Freedom
 +
*For e.g.,CHIINV(0.0257,3)
  
 
==Examples==
 
==Examples==

Revision as of 02:46, 16 June 2014

CHIINV(probability,degreesoffreedom)


  • Where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle probability} is the value associated with the Chi-squared Distribution
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle degreesoffreedom} is the number of Degrees of Freedom

Description

  • This function gives the inverse value of One_tailed probability of the Chi-squared Distribution.
  • It is called Inverted-Chi-square Distribution and it is a Continuous Probability Distribution of a positive-valued random variable.
  • Degrees of freedom Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle df} =.
  • The Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi^2} static used to compare the observed value in each table to the value which would be the expected under the assumption.
  • If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X} has the chi-squared distribution with n degrees of freedom, then according to the definition, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{X}} has the Inverse-chi-squared distribution with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} degrees of freedom;
  • If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle CHIDIST(x,df)=prob} , then Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle CHIINV(prob,df)= x} .
  • CHIINV use the iterating method to find the value of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} .suppose the iteration has not converged after 100 searches, then the function gives the error result.
  • This function will give the error result when
1.Any one of the arguments are non-numeric
2.Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle  df}
 value is not an integer
3.Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle  df < 1 }
or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle df>10^{10}}

4.Also Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle  prob < 0 }
 or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle prob>1}
.

ZOS Section

  • The syntax is to calculate CHIINV in ZOS is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle CHIINV(probability,degreesoffreedom)} .
    • Where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle probability} is the value associated with the Chi-squared Distribution
    • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle degreesoffreedom} is the number of Degrees of Freedom
  • For e.g.,CHIINV(0.0257,3)

Examples

  1. CHIINV(0.0001234098,2) = 18
  2. CHIINV(0.2547876,5) = 6.56699
  3. CHIINV(0.157299207050,1) = 2
  4. CHIINV(0.6785412,-1) = NAN

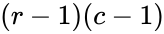See Also

References

Inverse-chi-squared Distribution

Retrieved from "http://wiki.zcubes.com/index.php?title=Manuals/calci/CHIINV&oldid=199659"