Difference between revisions of "Manuals/calci/LN"
Jump to navigation
Jump to search
| Line 6: | Line 6: | ||
*<math>LN</math> is the logarithm in which the base is the irrational number <math>e</math> (<math>e</math>= 2.71828...). | *<math>LN</math> is the logarithm in which the base is the irrational number <math>e</math> (<math>e</math>= 2.71828...). | ||
*For example, <math>ln_10 = loge_10 \approx 2.30258</math> | *For example, <math>ln_10 = loge_10 \approx 2.30258</math> | ||
| − | * | + | *It was formely also called Hyperbolic logarithm. |
| + | *And also called Napierian logarithm. | ||
*The constant <math>e</math> is called Euler's number. | *The constant <math>e</math> is called Euler's number. | ||
*The Natural Logarithm is denoted by <math>ln(x)</math> or <math>log e(x)</math>. | *The Natural Logarithm is denoted by <math>ln(x)</math> or <math>log e(x)</math>. | ||
Revision as of 23:39, 18 June 2014
LN(n)
- where is the positive real number.
Description
- This function gives the Natural Logarithm of a number.
- is the logarithm in which the base is the irrational number (= 2.71828...).
- For example, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ln_10 = loge_10 \approx 2.30258}
- It was formely also called Hyperbolic logarithm.
- And also called Napierian logarithm.
- The constant Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e} is called Euler's number.
- The Natural Logarithm is denoted by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ln(x)} or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle log e(x)} .
- where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} is the Positive real number.
- The Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ln(x)} is the inverse function of the exponential function Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{ln(x)}=x} if .
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ln(e^x)=x}
Examples
- =LN(15) = 2.708050201
- =LN(8.3) = 2.116255515
- =LN(1) = 0
- =LN(0) = INFINITY
- =LN(-20) = NAN
- =LN(exp(5)) = 5
- =EXP(LN(7)) = 7
 is the positive real number.
is the positive real number.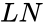 is the logarithm in which the base is the irrational number
is the logarithm in which the base is the irrational number 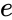 (
(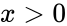 .
.