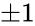Difference between revisions of "Manuals/calci/SIGNATURE"
Jump to navigation
Jump to search
| Line 20: | Line 20: | ||
==Examples== | ==Examples== | ||
| − | *1. MATRIX("signature") | + | *1. MATRIX("signature")= 1 |
| + | *2.MATRIX("signature",3) | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| Line 29: | Line 30: | ||
| 0 || 0 || 1 | | 0 || 0 || 1 | ||
|} | |} | ||
| − | * | + | *3.MATRIX("signature",6) |
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
Latest revision as of 01:40, 26 October 2015
MATRIX("SIGNATURE",order)
- is the size of the Signature matrix.
Description
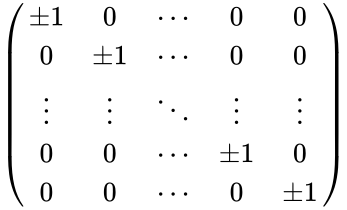
- This function returns the matrix of order 3 with the property of signature matrix.
- A signature matrix is a diagonal elements are
- So signature matrix is of the form:
- Any such matrix is its own inverse, hence is an involutory matrix.
- It is consequently a square root of the identity matrix.
- Also that not all square roots of the identity are signature matrices.
- The signature matrices are both symmetric and involutory,i.e.,they are orthogonal.
- Consequently, any linear transformation corresponding to a signature matrix constitutes an isometry.
Examples
- 1. MATRIX("signature")= 1
- 2.MATRIX("signature",3)
| 1 | 0 | 0 |
| 0 | -1 | 0 |
| 0 | 0 | 1 |
- 3.MATRIX("signature",6)
| 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | -1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | -1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 |
 is the size of the Signature matrix.
is the size of the Signature matrix.