Difference between revisions of "Manuals/calci/CIS"
Jump to navigation
Jump to search
| Line 5: | Line 5: | ||
*This function gives the CIS value. | *This function gives the CIS value. | ||
*CIS is another name for the complex exponential. | *CIS is another name for the complex exponential. | ||
| − | *<math>Cis(x)=e^{ix}=Cosx+i Sinx</math>, where <math>Cos</math> is the <math>Cosine</math> function,<math>i</math> is the imaginary unit and <math>Sin</math> is the <math>Sine</math>. | + | *<math>Cis(x)=e^{ix}=Cosx+i Sinx</math>, where <math>Cos</math> is the <math>Cosine</math> function,<math>i</math> is the imaginary unit and <math>Sin</math> is the <math>Sine</math> function. |
*Also <math> Cos(x)= \frac{e^{ix}+e^{-ix}}{2}</math>; | *Also <math> Cos(x)= \frac{e^{ix}+e^{-ix}}{2}</math>; | ||
* <math>Sin(x)=\frac{e^{ix}-e^{-ix}}{2i}</math> and <math>i^2</math>=-1. | * <math>Sin(x)=\frac{e^{ix}-e^{-ix}}{2i}</math> and <math>i^2</math>=-1. | ||
*So <math>Cis</math> abbreviates <math>Cos + i Sin</math>. | *So <math>Cis</math> abbreviates <math>Cos + i Sin</math>. | ||
| + | |||
| + | ==Examples== | ||
| + | #CIS(45) = 0.5253219888177297+i 0.8509035245341184 | ||
| + | #CIS(180) = -0.5984600690578581-i-0.8011526357338304 | ||
| + | #CIS(90.53) = -0.838546204483341+ⅈ0.5448304901036493 | ||
| + | |||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/SIN | SIN]] | ||
| + | *[[Manuals/calci/COS | COS ]] | ||
| + | |||
| + | |||
| + | ==References== | ||
| + | [http://mathworld.wolfram.com/Cis.html Complex Exponential] | ||
Revision as of 14:27, 22 December 2016
CIS (Theta)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Theta} is the angle value.
Description
- This function gives the CIS value.
- CIS is another name for the complex exponential.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Cis(x)=e^{ix}=Cosx+i Sinx} , where is the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Cosine} function,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} is the imaginary unit and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Sin} is the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Sine} function.
- Also Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Cos(x)= \frac{e^{ix}+e^{-ix}}{2}} ;
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Sin(x)=\frac{e^{ix}-e^{-ix}}{2i}} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i^2} =-1.
- So Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Cis} abbreviates Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Cos + i Sin} .
Examples
- CIS(45) = 0.5253219888177297+i 0.8509035245341184
- CIS(180) = -0.5984600690578581-i-0.8011526357338304
- CIS(90.53) = -0.838546204483341+ⅈ0.5448304901036493
See Also
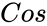 is the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Cosine}
function,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i}
is the imaginary unit and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Sin}
is the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Sine}
function.
is the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Cosine}
function,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i}
is the imaginary unit and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Sin}
is the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Sine}
function.