Difference between revisions of "Manuals/calci/HADAMARDPRODUCT"
| Line 7: | Line 7: | ||
*Hadamard product is also called Schur product or entrywise product. | *Hadamard product is also called Schur product or entrywise product. | ||
*The Hadamard product is associative,commutative and distributive. | *The Hadamard product is associative,commutative and distributive. | ||
| − | *Hadamard product is defined by,For two matrices, A and B, of the same dimension, mxn, the Hadamard product, <math> A\circ B</math, is a matrix, of the same dimension as the operands, with elements given by: | + | *Hadamard product is defined by,For two matrices, A and B, of the same dimension, mxn, the Hadamard product, <math> A\circ B</math>, is a matrix, of the same dimension as the operands, with elements given by: |
<math>(A \circ B)_{i,j}=(A)_{i,j}(B)_{i,j} </math> | <math>(A \circ B)_{i,j}=(A)_{i,j}(B)_{i,j} </math> | ||
*Hadamard Product of order 2 is calculated by: | *Hadamard Product of order 2 is calculated by: | ||
Revision as of 12:28, 7 June 2017
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b } are any two matrices.
Description
- This function shows the value of the Hadamard product.
- In Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle HADAMARDPRODUCT(a,b)} ,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} and are two matrices.
- Hadamard product is also called Schur product or entrywise product.
- The Hadamard product is associative,commutative and distributive.
- Hadamard product is defined by,For two matrices, A and B, of the same dimension, mxn, the Hadamard product, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A\circ B} , is a matrix, of the same dimension as the operands, with elements given by:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (A \circ B)_{i,j}=(A)_{i,j}(B)_{i,j} }
- Hadamard Product of order 2 is calculated by:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix}} Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \circ} Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{pmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{pmatrix}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{pmatrix} a_{11}b_{11} & a_{12}b_{12} \\ a_{21}b_{21} & a_{22}b_{22} \end{pmatrix}}
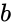 are two matrices.
are two matrices.