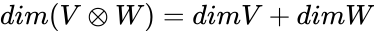Difference between revisions of "Manuals/calci/MATRIXTENSORPRODUCT"

Revision as of 13:31, 12 July 2017

MATRIXTENSORPRODUCT (a,b)

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} are any two matrices.

Description

This function shows the Tensor product of the matrix.
In Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle MATRIXTENSORPRODUCT (a,b)} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} are any two matrices.
Here matrices Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} should be square matrix with same order.
Tensor product is denoted by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \otimes} .
Tensor product is different from general product.
The Tensor product is defined by the product two vector spaces V and W is itself a Vector space.
It is denoted by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V\otimes W} .
The tensor product of V and W is the vector space generated by the symbols Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v\otimes w } , with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v \isin V} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w \isin W} .
The tensor product from the direct sum vector space, whose dimension is the sum of the dimensions of the two summands:

$dim(V\otimes W)=dimV+dimW$

Now consider any 2x2 matrices:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix}\otimes \begin{bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{bmatrix} = \begin{bmatrix} a_{11}\begin{bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{bmatrix} a_{12} \begin{bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{bmatrix} \\ a_{21} \begin{bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{bmatrix} a_{22} \begin{bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{bmatrix} \end{bmatrix} }

Difference between revisions of "Manuals/calci/MATRIXTENSORPRODUCT"

Revision as of 13:31, 12 July 2017

Description

Navigation menu

Search

@@ Line 9: / Line 9: @@
 *Tensor product is different from general product.
 *The Tensor product is defined by the product  two vector spaces V and W is itself a Vector space.
-*It is denoted by VSymbol W.
+*It is denoted by <math>V\otimes W</math>.
-*The tensor product of V and W is the vector space generated by the symbols  v\otimes w  v\otimes w, with  v belongs to V and w belongs to W.
+*The tensor product of V and W is the vector space generated by the symbols  <math>v\otimes w </math>, with  <math>v \isin V</math> and <math>w \isin W</math>.
-*The tensor product from the direct sum vector space, whose dimension is the sum of the dimensions of the two summands:Now consider any 2x2 matrices
+*The tensor product from the direct sum vector space, whose dimension is the sum of the dimensions of the two summands:
+<math>dim (V \otimes W)= dim V +dim W </math>
+*Now consider any 2x2 matrices:
+<math>\begin{bmatrix}
+a_{11}      & a_{12}     \\
+a_{21} & a_{22}
+\end{bmatrix}\otimes \begin{bmatrix}
+b_{11}      & b_{12}     \\
+b_{21} & b_{22}
+\end{bmatrix} =
+\begin{bmatrix}
+a_{11}\begin{bmatrix}
+b_{11}      & b_{12}     \\
+b_{21} & b_{22}
+\end{bmatrix}   a_{12} \begin{bmatrix}
+b_{11}      & b_{12}     \\
+b_{21} & b_{22}
+\end{bmatrix} \\
+a_{21} \begin{bmatrix}
+b_{11}      & b_{12}     \\
+b_{21} & b_{22}
+\end{bmatrix}
+a_{22} \begin{bmatrix}
+b_{11}      & b_{12}     \\
+b_{21} & b_{22}
+\end{bmatrix}
+\end{bmatrix} </math>