Manuals/calci/ACKERMANN
ACKERMANN(m,n)
- and are the positive integers.
Description
- The Ackermann function is a classic example of a recursive function, notable especially because it is not a primitive recursive function.
- All primitive recursive functions are total and computable, but the Ackermann function illustrates that not all total computable functions are primitive recursive.
- Its arguments are never negative and it always terminates.
- One common version, the two-argument Ackermann–Péter function, is defined as follows:
Failed to parse (unknown function "\begin{cases}"): {\displaystyle A(m,n) = \begin{cases} n+1 \mbox {if} \mbox {m=0} \\ A(m-1,1) & \mbox {if} \mbox {m>0} and \mbox {n=0} \\ A(m-1,A(m,n-1))& \mbox {if} \mbox {m>0} and \mbox {n>0} \end{cases} } for nonnegative integers m and n.
- Its value grows rapidly, even for small inputs.
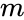 and
and  are the positive integers.
are the positive integers.