Manuals/calci/GFUNCTION
GFUNCTION (Number)
- is any positive real number.
Description
- This function shows the value of the Barnes G-function value.
- In Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle GFUNCTION (Number)} ,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Number} is any real number.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G(z)} is a function that is an extension of super factorials to the complex numbers.
- It is related to the Gamma function, the K-function and the Glaisher–Kinkelin constant, and was named after mathematician Ernest William Barnes.
- According to elementary factors, it is a special case of the double gamma function.
- Formally, the Barnes G-function is defined in the following Weierstrass product form:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G(1+z)={(2\pi)}^\frac{z}{2}exp(-\frac{z+z^2(1+\gamma)}{2})} Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \prod_{k=1}^\infty{{(1+\frac{z}{k}}^k exp(\frac {z^2}{2k}-z)}
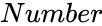 is any positive real number.
is any positive real number.