KURT(n1,n2,…)
- , are values to calculate kurtosis.
Description
- This function gives the value of Kurtosis of a given set.
- Kurtosis is the peak or flatness of a frequency distribution graph especially with respect to the concentration of values near the Mean as compared with the Normal Distribution.
- A normal distribution has a Kurtosis of 3.
- Distributions having higher Kurtosis have flatter tails or more extreme values that phenomenon called 'leptokurtosis' also it is the positive excess Kurtosis , and those with lower Kurtosis have fatter middles or fewer extreme value that phenomenon called 'Platykurtosis' also it is the negative excess Kurtosis.
- Example for positive Kurtosis(leptokurtosis) is Exponential distribution, Poisson distribution, Laplace Distribution.
- Example for Negative Kurtosis(platykurtosis) is Bernoulli distribution, Uniform distribution.
- Kurtosis has no units.
- Kurtosis is defined by:
- Kurtosis=:
, where is the Sample Standard Deviation. is the Arithmetic Mean.
- In this function arguments may be any type like numbers,names,arrays or references that contain numbers.
- We can give logical values and text references also directly.
- Suppose the referred argument contains any null cells, logical values like that values are not considered.
- This function will return the result as error when
1.Any one of the argument is non-numeric. 2.Suppose the number of data points are less than four or the standard deviation of the sample is zero 3.The referred arguments could not convert in to numbers.
- The below table is listing the Kurtosis excess for the number of common distributions:
| Distribution | Kurtosis excess | ||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bernoulli distribution | <math>\frac{1}{1-p}+\frac{1}{p}-6
Examples
See AlsoReferences |
 ,
,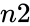 are values to calculate kurtosis.
are values to calculate kurtosis.