Manuals/calci/IMLOG
Jump to navigation
Jump to search
IMLOG (ComplexNumber,Base)
- is any complex number.
- is the base value of the Log.
Description
- This function shows the log value of a complex number.
- In , is any complex number.
- is the base value of a Log values.
- A complex logarithm function is an "inverse" of the complex exponential function.
- It is same as the real natural logarithm ln x is the inverse of the real exponential function.
- Thus, a logarithm of a complex number z is a complex number w such that .
- The notation for such a is or .
- If with which is in Polar form, then is one logarithm of z.
- Adding integer multiples of 2πi gives all the others.
- The complex exponential function is not injective, because Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{w+2\pi i} = e^w} for any w, since adding iθ to w has the effect of rotating Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^w} counterclockwise θ radians.
- So the points Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle .....w-4\pi i,w-2 \pi i, w, w+2\pi i,w+4 \pi i....}
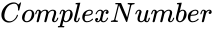 is any complex number.
is any complex number.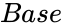 is the base value of the Log.
is the base value of the Log.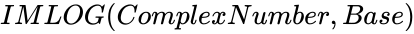 ,
,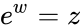 .
.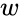 is
is 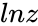 or
or 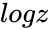 .
.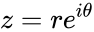 with
with 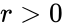 which is in Polar form, then
which is in Polar form, then 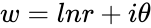 is one logarithm of z.
is one logarithm of z.