Manuals/calci/DIAGONALMATRIX
Jump to navigation
Jump to search
DIAGONALMATRIX(Order)
- is the size or order of the matrix.
Description
- This function shows the Diagonal matrix of a given order.
- In Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle DIAGONALMATRIX(Order)} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Order} is the order of square matrix.
- A diagonal matrix is a square matrix which is of the form Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{ij}=c_{i} \delta_{ij}} where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle delta_{ij}} is the Kronecker delta, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_{i}} are constants, and i,j=1, 2, ..., n.
- The general diagonal matrix is of the form:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{bmatrix} c_{1} & 0 & \cdots & 0 \\ 0 & c_{2} & \cdots & 0 \\ \vdots & \vdots &\ddots & \vdots \\ 0 & 0 & \cdots & c_{n} \end{bmatrix} } As stated above, the off-diagonal entries are zero. That is, the matrix A = (ai,j) with n columns and n rows is diagonal if
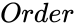 is the size or order of the matrix.
is the size or order of the matrix.