Manuals/calci/UNIFORMDISTRIBUTED
Jump to navigation
Jump to search
UNIFORMDISTRIBUTED (Numbers,Min,Max)
- is the number of variables.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Min} is the minimum value.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Max} is the maximum value.
Description
- This function shows the value of the Uniform distribution.
- In Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle UNIFORMDISTRIBUTED (Numbers,Min,Max)} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Numbers} is the number of variables.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Min} is the minimum value and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Max} is the maximum value.
- A uniform distribution, sometimes also known as a rectangular distribution.Uniform distribution has constant probability.
- The probability density function and cumulative distribution function for a continuous uniform distribution on the interval Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [a,b]} are
Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle P(x)={\begin{cases}0&forx<a\\{\frac {1}{b-a}}&fora\leq x\leq b\\0&forx>b\end{cases}}}
Examples
1. UNIFORMDISTRIBUTED(3,2,7) = 6.659664455776188 6.990120242068037 2.4882508586819068 2. UNIFORMDISTRIBUTED(1..3,-2,0)
| Numbers | Min | Max | UNIFORMDISTRIBUTED |
|---|---|---|---|
| 1 | -2 | 0 | -0.38819952844254946 |
| 2 | -2 | 0 | -1.628112389920573 -1.7184357400573753 |
| 3 | -2 | 0 | -0.26144691128294006 -0.09738283572669815 -1.0603991883330703 |
Numbers Min Max UNIFORMDISTRIBUTED 1 -2 0 -0.38819952844254946 2 -2 0 -1.628112389920573 -1.7184357400573753 3 -2 0 -0.26144691128294006 -0.09738283572669815 -1.0603991883330703
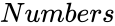 is the number of variables.
is the number of variables.