Manuals/calci/CHIDIST
CHIDIST(x,df)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} is the value for which distribution is evaluated.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle df} is the number of degrees of freedom.
Description
- This function gives the one_tailed probability of the chi-squared distribution.
- It is denoted by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi^2} distribution.
- Normally categorical data's may displayed in tables. The static used to compare the observed value in each table to the value which would be the expected under the assumption.
- The conditions of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi^2} test is
- The table should be 2x2 or more than 2x2
- Each observations should not be dependent
- All expected values should be 10 or greater.
- The test statistic is:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi^2=\sum\frac{(Oi-Ei)^2}{Ei}}
The degrees of freedom are: (r–1)(c–1)
- r = No. of rows
- c = No. of columns
Where:
- Oi-the observed value in the ith cell
- Ei- the expected value in the ith cell
Also this function will the result as Error when
- The x & df values are non-numeric
- The x value is negative or df value is not an integer
- The df <1 or df>10^10
- Here CHIDIST=P(X>x),where X is a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi^2} random variable.
- CHIDIST(-2,1)=Error, because x is negative.
- CHIDIST(2,-1)=Error, because df<1
Examples
| CHIDIST(x,df) | x | df | RESULT |
|---|---|---|---|
| CHIDIST(18,2) | 18 | 2 | 0.0001234098 |
| CHIDIST(15,1) | 15 | 1 | 0.0001075112 |
| CHIDIST(2,1) | 2 | 1 | 0.157299207050 |
| CHIDIST(-2,1) | (-2) | 1 | error |
| CHIDIST(2,-1) | 2 | (-1) | error |
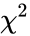 static used to compare the observed value in each table to the value which would be the expected under the assumption.
static used to compare the observed value in each table to the value which would be the expected under the assumption.