Manuals/calci/PASCAL

MATRIX("PASCAL",order)

• Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle order} is the size of the Pascal matrix.

Description

• This function returns the matrix of any order with the property of Pascal.
• The Pascal matrix is an infinite matrix containing the binomial coefficients as its elements.
• To obtain a pascal matrix there are three ways: as either an upper-triangular matrix(U), a lower-triangular matrix(L), or a symmetric matrix(S).
• Example for these matrices are:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_4 =\begin{pmatrix} 54 & 0 & 0 & 0 \\ 20 & 34 & 0 & 0 \\ 57 & 89 & -70 & 0 \\ 71 & -4 & -52 & 72 \\ \end{pmatrix}} Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_4 =\begin{pmatrix} 64 & 22 & -91 & -86 \\ 0 & 61 & 62 & -62 \\ 0 & 0 & 30 & -81 \\ 0 & 0 & 0 & -61 \\ \end{pmatrix}} Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_4 =\begin{pmatrix} 41 & 74 & 15 & -47 \\ 74 & -16 & 37 & 97 \\ 15 & 37 & 24 & -88 \\ -47 & 97 & -88 & -69 \\ \end{pmatrix}}

• The amazing relationship of these matrices are:Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_n = L_nU_n} .
• And its determinants also 1.i.e.,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |S_n|=|L_n|=|U_n|=1 }
• The Pascal matrix can actually be constructed by taking the matrix exponential of a special subdiagonal or superdiagonal matrix.
• The elements of the symmetric Pascal matrix are the binomial coefficients, i.e.

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{ij} = {n \choose r} = \frac{n!}{r!(n-r)!},} , where n=i+j, r=i.

• In other words,

$S_{ij}=_{i+j}{C}_{i}={\frac {(i+j)!}{(i)!(j)!}}$.

• Here MATRIX("pascal") is showing the pascal matrix of order 3.
• So users can change the order of the matrix also.
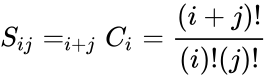