Difference between revisions of "Manuals/calci/ACKERMANN"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:30px">'''BETADIST(x,alpha,beta,a,b)'''</div><br/> *<math>x</math> is the value between <math>a</math> and <math>b</math> *alpha and beta are the value of...") |
|||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">''' | + | <div style="font-size:30px">'''ACKERMANN(m,n)'''</div><br/> |
| − | *<math> | + | *<math>m</math> and <math>n</math> are the positive integers. |
| − | |||
| − | |||
==Description== | ==Description== | ||
| + | *The Ackermann function is a classic example of a recursive function, notable especially because it is not a primitive recursive function. | ||
| + | *All primitive recursive functions are total and computable, but the Ackermann function illustrates that not all total computable functions are primitive recursive. | ||
| + | *Its arguments are never negative and it always terminates. | ||
| + | *One common version, the two-argument Ackermann–Péter function, is defined as follows: | ||
| + | <math>A(m,n) = \begin{cases} n+1 if m=0 \\ | ||
| + | A(m-1,1) & \mbox {if} m>0 and n=0 \\ | ||
| + | A(m-1,A(m,n-1))& \mbox {if} m>0 and n>0 | ||
| + | \end{cases}</math> | ||
| + | for nonnegative integers m and n. | ||
| + | *Its value grows rapidly, even for small inputs. | ||
Revision as of 14:03, 21 September 2016
ACKERMANN(m,n)
- and are the positive integers.
Description
- The Ackermann function is a classic example of a recursive function, notable especially because it is not a primitive recursive function.
- All primitive recursive functions are total and computable, but the Ackermann function illustrates that not all total computable functions are primitive recursive.
- Its arguments are never negative and it always terminates.
- One common version, the two-argument Ackermann–Péter function, is defined as follows:
for nonnegative integers m and n.
- Its value grows rapidly, even for small inputs.
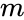 and
and  are the positive integers.
are the positive integers.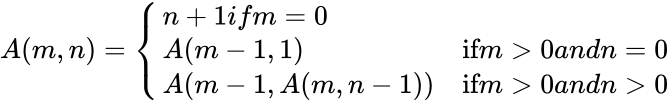 for nonnegative integers m and n.
for nonnegative integers m and n.