Difference between revisions of "Manuals/calci/FDIST"
Jump to navigation
Jump to search
| (16 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''FDIST( | + | <div style="font-size:30px">'''FDIST (Number,DegreeOfFreedom1,DegreeOfFreedom2)'''</div><br/> |
| − | *<math> | + | *<math>Number</math> is the value of the function |
| − | *<math> | + | *<math>DegreeOfFreedom1</math> and <math>DegreeOfFreedom2</math> are numbers of degrees of freedom. |
| + | **FDIST(), returns the F probability distribution. | ||
==Description== | ==Description== | ||
| Line 7: | Line 8: | ||
*This distribution is continuous probability distribution and it is called Fisher-Snedecor distribution. | *This distribution is continuous probability distribution and it is called Fisher-Snedecor distribution. | ||
*The F distribution is an asymmetric distribution that has a minimum value of 0, but no maximum value. | *The F distribution is an asymmetric distribution that has a minimum value of 0, but no maximum value. | ||
| − | *In <math>FDIST( | + | *In <math>FDIST (Number,DegreeOfFreedom1,DegreeOfFreedom2), Number </math> is the value of the function ,<math>DegreeOfFreedom1</math> is the numerator degrees of freedom and <math>DegreeOfFreedom2</math> is the denominator degrees of freedom. |
*This distribution is the ratio of two chi-square distributions with degrees of freedom r1 and r2, respectively, where each chi-square has first been divided by its degrees of freedom. | *This distribution is the ratio of two chi-square distributions with degrees of freedom r1 and r2, respectively, where each chi-square has first been divided by its degrees of freedom. | ||
*The Probability density function of the F distribution is: | *The Probability density function of the F distribution is: | ||
<math>f(x,r_1,r_2)=\frac{\Gamma[\frac{r_1+r_2}{2}](\frac{r_1}{r_2})^{\tfrac{r_1}{2}}}{ \Gamma(\frac{r_1}{2})\Gamma(\frac{r_2}{2})}*\frac{(x)^{\tfrac{r_1}{2}-1}}{(\frac{1+r_1x}{r_2})^{\tfrac{r_1+r_2}{2}}}</math> | <math>f(x,r_1,r_2)=\frac{\Gamma[\frac{r_1+r_2}{2}](\frac{r_1}{r_2})^{\tfrac{r_1}{2}}}{ \Gamma(\frac{r_1}{2})\Gamma(\frac{r_2}{2})}*\frac{(x)^{\tfrac{r_1}{2}-1}}{(\frac{1+r_1x}{r_2})^{\tfrac{r_1+r_2}{2}}}</math> | ||
| − | 0<x<\infty</math> where | + | <math>0<x<\infty</math> where <math>\Gamma</math> is the Gamma Function. |
| − | *The gamma function is defined by Gamma(t) = | + | *The gamma function is defined by <math>\Gamma(t) = \int\limits_{0}^{\infty} x^{t-1} e^{-x} dx</math>. |
| − | When the value of | + | When the value of DegreeOfFreedom1 and DegreeOfFreedom2 are not integers ,then it is converted in to integers. |
*This function will give the result as error when | *This function will give the result as error when | ||
| − | 1. any one of the argument is | + | 1. any one of the argument is non-numeric. |
| − | 2. | + | 2. Number is negative |
| − | 3. | + | 3. If DegreeOfFreedom1<1 or DegreeOfFreedom2><math>10^{10}</math> and DegreeOfFreedom2<1 or DegreeOfFreedom2> <math>10^{10}</math> |
| + | |||
| + | ==ZOS== | ||
| + | |||
| + | *The syntax is to find FDIST in ZOS is <math>FDIST (Number,DegreeOfFreedom1,DegreeOfFreedom2)</math>. | ||
| + | **<math>Number</math> is the value of the function. | ||
| + | *For e.g.,FDIST(85.2,22,18) | ||
| + | *FDIST(67..70,6,8) | ||
==Examples== | ==Examples== | ||
| − | #FDIST(20.6587,7,3)=0.01526530981 | + | #=FDIST(20.6587,7,3) = 0.01526530981 |
| − | #FDIST(70.120045,12.2,6.35)=0.000011229898 | + | #=FDIST(70.120045,12.2,6.35) = 0.000011229898 |
| − | #FDIST(10,1.3,1.5)=0. | + | #=FDIST(10,1.3,1.5) = 0.12923064798773362 |
| − | #FDIST(-28,4,6)= | + | #=FDIST(-28,4,6) = #N/A (NUMBER > 0) |
| + | ==Related Videos== | ||
| + | {{#ev:youtube|7rGAh_XDvY8|280|center|F Distribution}} | ||
==See Also== | ==See Also== | ||
*[[Manuals/calci/FINV | FINV ]] | *[[Manuals/calci/FINV | FINV ]] | ||
| − | *[[Manuals/calci/FTEST | FTEST ]] | + | *[[Manuals/calci/FTEST | FTEST ]] |
| + | |||
| + | ==References== | ||
| + | [http://en.wikipedia.org/wiki/F-distribution F-Distribution] | ||
| − | + | *[[Z_API_Functions | List of Main Z Functions]] | |
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 10:10, 2 June 2020
FDIST (Number,DegreeOfFreedom1,DegreeOfFreedom2)
- is the value of the function
- and are numbers of degrees of freedom.
- FDIST(), returns the F probability distribution.
Description
- This function gives the value of F probability distribution.
- This distribution is continuous probability distribution and it is called Fisher-Snedecor distribution.
- The F distribution is an asymmetric distribution that has a minimum value of 0, but no maximum value.
- In is the value of the function , is the numerator degrees of freedom and is the denominator degrees of freedom.
- This distribution is the ratio of two chi-square distributions with degrees of freedom r1 and r2, respectively, where each chi-square has first been divided by its degrees of freedom.
- The Probability density function of the F distribution is:
where is the Gamma Function.
- The gamma function is defined by .
When the value of DegreeOfFreedom1 and DegreeOfFreedom2 are not integers ,then it is converted in to integers.
- This function will give the result as error when
1. any one of the argument is non-numeric. 2. Number is negative 3. If DegreeOfFreedom1<1 or DegreeOfFreedom2> and DegreeOfFreedom2<1 or DegreeOfFreedom2>
ZOS
- The syntax is to find FDIST in ZOS is .
- is the value of the function.
- For e.g.,FDIST(85.2,22,18)
- FDIST(67..70,6,8)
Examples
- =FDIST(20.6587,7,3) = 0.01526530981
- =FDIST(70.120045,12.2,6.35) = 0.000011229898
- =FDIST(10,1.3,1.5) = 0.12923064798773362
- =FDIST(-28,4,6) = #N/A (NUMBER > 0)
Related Videos
See Also
References
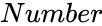 is the value of the function
is the value of the function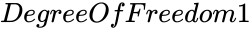 and
and 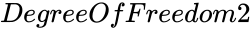 are numbers of degrees of freedom.
are numbers of degrees of freedom.
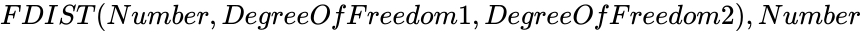 is the value of the function ,
is the value of the function ,^{\tfrac {r_{1}}{2}}}{\Gamma ({\frac {r_{1}}{2}})\Gamma ({\frac {r_{2}}{2}})}}*{\frac {(x)^{{\tfrac {r_{1}}{2}}-1}}{({\frac {1+r_{1}x}{r_{2}}})^{\tfrac {r_{1}+r_{2}}{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/png/bf128c19052b2d77e9867508e60f25c553dfee41)
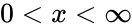 where
where 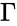 is the Gamma Function.
is the Gamma Function.
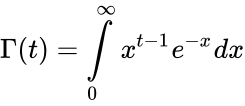 .
.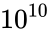 and DegreeOfFreedom2<1 or DegreeOfFreedom2>
and DegreeOfFreedom2<1 or DegreeOfFreedom2> 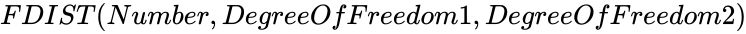 .
.