Difference between revisions of "Manuals/calci/KSTESTCORE"
Jump to navigation
Jump to search
(Created page with "==Ks") |
|||
| (7 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | == | + | <div style="font-size:25px">'''KSTESTCORE (XRange,ObservedFrequency,Confidence,NewTableFlag,Test,DoMidPointOfIntervals)'''</div><br/> |
| + | |||
| + | *<math>XRange</math> is the set of values. | ||
| + | |||
| + | ==Description== | ||
| + | *This function gives the test statistic of the K-S test. | ||
| + | *K-S test is indicating the Kolmogorov-Smirnov test. | ||
| + | *It is one of the non parametric test. | ||
| + | *This test is the equality of continuous one dimensional probability distribution. | ||
| + | *It can be used to compare sample with a reference probability distribution or to compare two samples. | ||
| + | *This test statistic measures a distance between the empirical distribution function of the sample and the cumulative distribution function of the reference distribution, or between the empirical distribution functions of two samples. | ||
| + | *The two-sample KS test is one of the most useful and general nonparametric methods for comparing two samples. | ||
| + | *It is sensitive to differences in both location and shape of the empirical cumulative distribution functions of the two samples. | ||
| + | *This test can be modified to serve as a goodness of fit test. | ||
| + | *The assumption of the KS test is: | ||
| + | *Null Hypothesis(H0):The sampled population is normally distributed. | ||
| + | *Alternative hypothesis(Ha):The sampled population is not normally distributed. | ||
| + | *The Kolmogorov-Smirnov test to compare a data set to a given theoretical distribution is as follows: | ||
| + | *1.Data set sorted into increasing order and denoted as <math>x_i</math>, where i=1,...,n. | ||
| + | *2.Smallest empirical estimate of fraction of points falling below <math>x_i</math>, and computed as <math>\frac{(i-1)}{n}</math> for i=1,...,n. | ||
| + | *3.Largest empirical estimate of fraction of points falling below <math>x_i</math> and computed as <math>\frac{i}{n}</math> for i=1,...,n. | ||
| + | *4.Theoretical estimate of fraction of points falling below <math>x_i</math> and computed as <math>F(x_i)</math>, where F(x) is the theoretical distribution function being tested. | ||
| + | *5.Find the absolute value of difference of Smallest and largest empirical value with the theoretical estimation of points. | ||
| + | *This is a measure of "error" for this data point. | ||
| + | *6.From the largest error, we can compute the test statistic. | ||
| + | *The Kolmogorov-Smirnov test statistic for the cumulative distribution F(x) is:<math> D_n=Sup_x|F_n(x)-F(x)|</math>where <math>sup_x</math> is the supremum of the set of distances. | ||
| + | *<math>F_n(x)</math> is the empirical distribution function for n,with the observations <math>X_i</math> is defined as:<math>F_n(x)= Refer Wikipedia I_{X_i\le x}</math>where <math>I_{X_i\le x}</math> is the indicator function, equal to 1 if <math>X_i\le x</math> and equal to 0 otherwise. | ||
| + | * Using this function we can identify the following deatils: | ||
| + | Are the data from the Normal distribution or Weibull distribution or Exponential distribution or a logistic distribution. | ||
| + | |||
| + | ==Examples== | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=cltWQsmBg0k&t=108s|280|center|Kolmogorov-Smirnov Test }} | ||
| + | |||
| + | ==See Also== | ||
| + | |||
| + | *[[Manuals/calci/KSTESTNORMAL| KSTESTNORMAL]] | ||
| + | *[[Manuals/calci/LEVENESTEST| LEVENESTEST]] | ||
| + | *[[Manuals/calci/MOODSMEDIANTEST| MOODSMEDIANTEST]] | ||
| + | |||
| + | ==References== | ||
| + | [http://www.itl.nist.gov/div898/handbook/eda/section3/eda35g.htm KS Test] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 15:04, 6 December 2018
KSTESTCORE (XRange,ObservedFrequency,Confidence,NewTableFlag,Test,DoMidPointOfIntervals)
- is the set of values.
Description
- This function gives the test statistic of the K-S test.
- K-S test is indicating the Kolmogorov-Smirnov test.
- It is one of the non parametric test.
- This test is the equality of continuous one dimensional probability distribution.
- It can be used to compare sample with a reference probability distribution or to compare two samples.
- This test statistic measures a distance between the empirical distribution function of the sample and the cumulative distribution function of the reference distribution, or between the empirical distribution functions of two samples.
- The two-sample KS test is one of the most useful and general nonparametric methods for comparing two samples.
- It is sensitive to differences in both location and shape of the empirical cumulative distribution functions of the two samples.
- This test can be modified to serve as a goodness of fit test.
- The assumption of the KS test is:
- Null Hypothesis(H0):The sampled population is normally distributed.
- Alternative hypothesis(Ha):The sampled population is not normally distributed.
- The Kolmogorov-Smirnov test to compare a data set to a given theoretical distribution is as follows:
- 1.Data set sorted into increasing order and denoted as , where i=1,...,n.
- 2.Smallest empirical estimate of fraction of points falling below , and computed as for i=1,...,n.
- 3.Largest empirical estimate of fraction of points falling below and computed as for i=1,...,n.
- 4.Theoretical estimate of fraction of points falling below and computed as , where F(x) is the theoretical distribution function being tested.
- 5.Find the absolute value of difference of Smallest and largest empirical value with the theoretical estimation of points.
- This is a measure of "error" for this data point.
- 6.From the largest error, we can compute the test statistic.
- The Kolmogorov-Smirnov test statistic for the cumulative distribution F(x) is:where is the supremum of the set of distances.
- is the empirical distribution function for n,with the observations is defined as:where is the indicator function, equal to 1 if and equal to 0 otherwise.
- Using this function we can identify the following deatils:
Are the data from the Normal distribution or Weibull distribution or Exponential distribution or a logistic distribution.
Examples
Related Videos
See Also
References
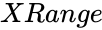 is the set of values.
is the set of values.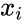 , where i=1,...,n.
, where i=1,...,n.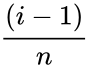 for i=1,...,n.
for i=1,...,n.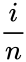 for i=1,...,n.
for i=1,...,n.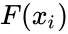 , where F(x) is the theoretical distribution function being tested.
, where F(x) is the theoretical distribution function being tested.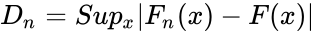 where
where 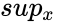 is the supremum of the set of distances.
is the supremum of the set of distances.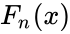 is the empirical distribution function for n,with the observations
is the empirical distribution function for n,with the observations 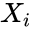 is defined as:
is defined as: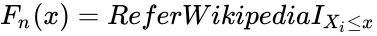 where
where 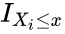 is the indicator function, equal to 1 if
is the indicator function, equal to 1 if 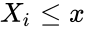 and equal to 0 otherwise.
and equal to 0 otherwise.