Manuals/calci/ZTEST
ZTEST (Array,Mean,StandardDeviationForPopulation,IsTwoTailed,Accuracy)
- is the set of values.
- is the mean value.
- is the standard deviation of the population.
- is the value of the tail.
- gives accurate value of the solution.
- ZTEST() returns the one-tailed probability-value of a z-test.
Description
- This function gives the one-tailed probability of z-test.
- Z-test is used to determine whether two population means are different when the variances are known and the sample size is large.
- In , is the array of values against which the hypothesized sample mean is to be tested.
- is the hypothesized sample mean, and is the standard deviation of the population.
- When we are not giving the sigma value, it will use the standard deviation of sample.
- This function returns the probability that the supplied hypothesized sample mean is greater than the mean of the supplied data values.
- The test statistic should follow a normal distribution.
- ZTEST is calculated when sigma is not omitted and x=μ0 :
- ZTEST is calculated when sigma is omitted and x=μ0:
where is sample mean , is the sample deviation and is the size of the sample.
- Suppose we want to calculate the z-test for two tailed probability then this can be done by using the Z_test function: .
- This function will give the result as error when
1. Any one of the argument is non-numeric.
2. Array or Mean value is empty.
3. Array contains only one value.
Examples
- Example 1
| A | B | C | D | E | F | G | |
|---|---|---|---|---|---|---|---|
| 1 | 10 | 15 | 7 | 2 | 19 | 20 | 12 |
| 2 | 3 | 4 | 8 | 1 | 10 | 15 | 5 |
- =ZTEST(A1:G1,4) = 0.00042944272036
- =2*MIN(ZTEST(A1:G1,4),1-ZTEST(A1:G1,4)) = 0.000858885440
- =ZTEST(A2:F2,10) = 0.9708451547030459
- =2*MIN(ZTEST(A2:F2,10),1-ZTEST(A2:F2,10)) = 0.058309690593908226
Related Videos
See Also
References
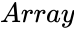 is the set of values.
is the set of values.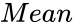 is the mean value.
is the mean value.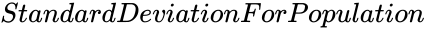 is the standard deviation of the population.
is the standard deviation of the population.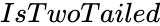 is the value of the tail.
is the value of the tail.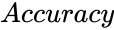 gives accurate value of the solution.
gives accurate value of the solution.
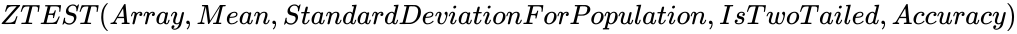 ,
,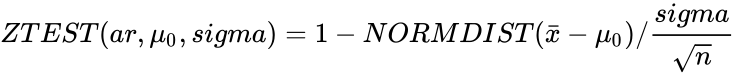
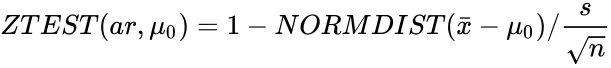 where
where 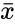 is sample mean ,
is sample mean , 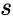 is the sample deviation and
is the sample deviation and  is the size of the sample.
is the size of the sample.
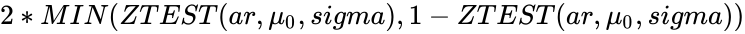 .
.