Manuals/calci/hankel
HANKEL(Number)
- is the order of the hankel matrix.
Description
- This function gives the matrix with the property of hankel matrix with the given order.
- A hankel matrix is a square matrix with constant skew diagonals.
- If the i,j element of Hankel matrix A is denoted , then we have
.
- i.e., The form of Hankel matrix is:
.
- A hankel matrix is also called as catalecticant matrix.
- Here HANKEL(3) is gives the hankel matrix of order 3 with decimal values.
- A Hankel matrix is an upside-down Toeplitz matrix.
- A matrix whose entries along a parallel to the main anti-diagonal are equal, for each parallel.
- Sometimes this type of matrices are also called as orthosymmetric matrices.
Examples
1. hankel(2)
| 0.8035830636448866 | 0.8035830636448866 |
| 0.8035830636448866 | 0.001881340454530589 |
2. HANKEL(4)
| 0.3661268740416319 | 0.041098489444291175 | 0.5811984241396517 | 0.5811984241396517 |
| 0.041098489444291175 | 0.5811984241396517 | 0.5811984241396517 | 0.041098489444291175 |
| 0.5811984241396517 | 0.5811984241396517 | 0.041098489444291175 | 0.3661268740416319 |
| 0.5811984241396517 | 0.041098489444291175 | 0.3661268740416319 | 0.06363525915203883 |
Related Videos
See Also
References
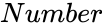 is the order of the hankel matrix.
is the order of the hankel matrix.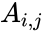 , then we have
, then we have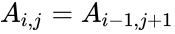 .
.
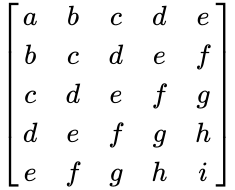 .
.