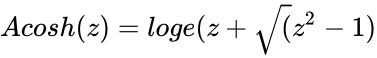Difference between revisions of "Manuals/calci/ACOSH"
Jump to navigation
Jump to search
| Line 6: | Line 6: | ||
*Here 'z' is any positive real number i.e, z >= 1 . | *Here 'z' is any positive real number i.e, z >= 1 . | ||
*Inverse Hyperbolic sine of a number is defined by <math>Acosh(z)=log e(z+\sqrt(z^2-1)</math> | *Inverse Hyperbolic sine of a number is defined by <math>Acosh(z)=log e(z+\sqrt(z^2-1)</math> | ||
| + | *ACOSH(-2)=NAN , since z>2 | ||
== Examples == | == Examples == | ||
Revision as of 00:05, 6 November 2013
ACOSH(z)
- where z is any real number
Description
- This function gives the Inverse Hyperbolic Cosine of a number.
- Here 'z' is any positive real number i.e, z >= 1 .
- Inverse Hyperbolic sine of a number is defined by
- ACOSH(-2)=NAN , since z>2
Examples
ACOSH(z)
- z is any real number.
| ACOSH(z) | Value(Radian) |
| ACOSH(1) | 0 |
| ACOSH(30) | 4.0940666863209 |
| ACOSH(90) | 5.192925985263806 |