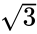Difference between revisions of "Manuals/calci/TAN"
Jump to navigation
Jump to search
| Line 12: | Line 12: | ||
Consider '''x = 60''' then '''=TAN(RADIANS(60))''' gives '''1.7320508075688767''' that is similar to <math>\sqrt{3}</math> <br/> | Consider '''x = 60''' then '''=TAN(RADIANS(60))''' gives '''1.7320508075688767''' that is similar to <math>\sqrt{3}</math> <br/> | ||
The above function gives the Tangent of 'x' in Degree.<br/> | The above function gives the Tangent of 'x' in Degree.<br/> | ||
| − | *In a right angled triangle, '''TAN = Opposite / Adjacent''' or '''SIN / COS'''.<br/> | + | *In a right angled triangle, '''TAN = Opposite side / Adjacent side''' or '''SIN / COS'''.<br/> |
*TAN function determines the Tangent of the given angle. | *TAN function determines the Tangent of the given angle. | ||
*By default, Calci takes the angle in Radians. | *By default, Calci takes the angle in Radians. | ||
Revision as of 01:52, 6 November 2013
TAN(x)
- where x is the angle in Radians
- by default, Calci use angle in Radians
DTAN can be used if the angle is in degrees.
The angle can be a single value or any complex array of values.
For example TAN(1..100) can give an array of the results, which is the TAN value for each of the elements in the array. The array could be of any values either '+' or '-' like 1..5@TAN or (-5)..(-1)@TAN.
Description
Consider x = 60 then =TAN(RADIANS(60)) gives 1.7320508075688767 that is similar to
The above function gives the Tangent of 'x' in Degree.
- In a right angled triangle, TAN = Opposite side / Adjacent side or SIN / COS.
- TAN function determines the Tangent of the given angle.
- By default, Calci takes the angle in Radians.
- To convert Radians to Degrees, multiply with 180/PI() or we have to use the Radians function like TAN(RADIANS(x)) or DTAN(x)
The following example shows how TAN is applied to an array of numbers containing angles 1..10.
1..10@TAN
| Angles | TAN |
|---|---|
| 1 | 1.55740772465 |
| 2 | -2.18503986326 |
| 3 | -0.14254654307 |
| 4 | 1.15782128235 |
| 5 | -3.38051500625 |
| 6 | -0.29100619138 |
| 7 | 0.87144798272 |
| 8 | -6.79971145522 |
| 9 | -0.45231565944 |
| 10 | 0.64836082745 |
Examples
TAN(x)
- x is the angle in Radians.
| TAN(Radian) | Value |
| TAN(0) | 0 |
| TAN(1) | 1.55740772465 |
| TAN(90) | -1.99520041221 |