Difference between revisions of "Manuals/calci/ATAN2"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
| + | <div style="font-size:30px">'''ATAN2'''</div><br/> | ||
| + | * where 'iz' is the complex number | ||
| + | ==Description== | ||
| − | < | + | *This function gives the cos value of 'iz'. |
| + | *Where iz is the complex number in the form of <math>x+iy</math> | ||
| + | *x & y are the real number | ||
| + | *'i' is the imaginary unit <math>i=\sqrt{-1}</math> | ||
| + | *Also x is called the real part & y is the imaginary patr of a complex number. | ||
| + | *'COMPLEX' is the function used to convert Real & Imaginary numbers in to a complex number. | ||
| + | *<math>cos(x+iy)</math> is defined by <math>cos(x+iy)=cos(x)cosh(y)-isin(x)sinh(y)</math> | ||
| − | + | == Examples == | |
| + | '''IMCOS(iz)''' | ||
| + | *'''iz''' is the complex number. | ||
| − | + | {|id="TABLE1" class="SpreadSheet blue" | |
| − | |||
| − | |||
| − | + | |- class="even" | |
| + | |'''IMCOS(iz)''' | ||
| + | |'''Value(Radian)''' | ||
| − | + | |- class="odd" | |
| − | + | | IMCOS("2+3i") | |
| − | + | | -4.189-i9.109 | |
| − | + | |- class="even" | |
| + | | IMCOS("2-3i") | ||
| + | | 4.189-i9.109 | ||
| − | + | |- class="odd" | |
| − | + | | IMCOS("2") | |
| − | + | | 0.4161468 | |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==See Also== | |
| − | + | *[[Manuals/calci/COS| COS]] | |
| − | |||
| − | |||
| − | + | *[[Manuals/calci/COMPLEX| COMPLEX]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==References== | |
| − | |||
| − | |||
| − | + | *[http://en.wikipedia.org/wiki/Trigonometric_functions List of Trigonometric Functions] | |
| + | *[http://en.wikipedia.org/wiki/Hyperbolic_function Hyperbolic Function] | ||
| − | |||
| − | |||
| − | |||
| − | </ | + | Where xn is the x-coordinate and yn is the y-coordinate of that particular point |
| − | --- | + | ATAN2 returns the error value when both xn and yn are 0. </font></font> |
| − | + | If you want to convert the arctangent in degrees, multiply the result by 180/PI. | |
| + | Calci returns the arctangent of the particular x- and y-coordinates. It is the angle from the x-axis to a line with origin (0, 0) and with coordinates (xn, yn). | ||
Revision as of 03:08, 6 November 2013
ATAN2
- where 'iz' is the complex number
Description
- This function gives the cos value of 'iz'.
- Where iz is the complex number in the form of
- x & y are the real number
- 'i' is the imaginary unit
- Also x is called the real part & y is the imaginary patr of a complex number.
- 'COMPLEX' is the function used to convert Real & Imaginary numbers in to a complex number.
- is defined by
Examples
IMCOS(iz)
- iz is the complex number.
| IMCOS(iz) | Value(Radian) |
| IMCOS("2+3i") | -4.189-i9.109 |
| IMCOS("2-3i") | 4.189-i9.109 |
| IMCOS("2") | 0.4161468 |
See Also
References
Where xn is the x-coordinate and yn is the y-coordinate of that particular point
ATAN2 returns the error value when both xn and yn are 0.
If you want to convert the arctangent in degrees, multiply the result by 180/PI.
Calci returns the arctangent of the particular x- and y-coordinates. It is the angle from the x-axis to a line with origin (0, 0) and with coordinates (xn, yn).
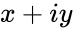
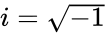
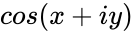 is defined by
is defined by