Difference between revisions of "Manuals/calci/COT"

From ZCubes Wiki
Jump to navigation Jump to search
 
(32 intermediate revisions by 3 users not shown)
Line 1: Line 1:
−
<div style="font-size:30px">'''COT(x)'''</div><br/>
+
=Demo Study Page=
−
* where '''x''' is in Radians
 
−
* by default Calci use Radian as angle
 
  
−
[[Manuals/calci/DTAN | DTAN]] can be used if the angle is in degrees.  
+
* Where x is the number and it is varying from -1 to 1.
 +
* The value of ASIN(x) is in radians in the range -pi()/2 to pi()/2.
 +
* Calci returns the value of arcsine (inverse sine)is in Radians.
 +
*The number can be a single value or any number of values.
  
−
The angle can be a single value or any complex array of values.
+
For example, ASIN(0.5,(-0.2),1) gives the arcsine or inversesine values for each element.
  
−
For example TAN(1..100) can give an array of the results, which is the TAN value for each of the elements in the array. The array could be of any shape.
+
== Description ==
  
−
==Description==
+
Consider x = (-0.8) then, ASIN((-0.8))'' is -0.9273
−
Consider &nbsp;&nbsp;&nbsp; '''x = 90'''&nbsp;&nbsp;&nbsp;  then &nbsp;&nbsp;&nbsp;  '''=TAN(RADIANS(90))'''&nbsp;&nbsp;&nbsp; gives &nbsp;&nbsp;&nbsp;'''1''' <br/>
+
*This function is the Inverse function of Sin in trigonometry.
−
*This function gives the tangent of 'x'.
+
*It's also called as Cyclometric function.
−
*In a right angled triangle, '''TAN = Opposite / Adjacent''' or '''SIN / COS'''.<br/>
+
*ASIN is described as Arcsin of a given number and denoted by <math>sin^{-1}</math>(x).
−
*By default, Calci takes the angle in Radians.
+
*In  ASIN(x) ,x value should be with in -1 & 1.
−
*To convert Radian to Degree, multiply with 180/PI() or we have to use the Radians function like TAN(RADIANS(x))
+
*To find the angle in degrees, multiply the result angle with 180/PI().
 +
*DEGREES function can also be used.
  
−
The following example shows how TAN is applied to an array of numbers containing numbers 1..10.
+
For example ASIN(-0.8)*180/PI() or DEGREES(ASIN(-0.8))'' gives -53.13010235415598
−
 
 
−
1..10@TAN
 
−
 
 
−
{| class="wikitable"
 
−
|-
 
−
! Number !! TAN
 
−
|-
 
−
| 1 || 1.55740772465
 
−
|-
 
−
| 2 || -2.18503986326
 
−
|-
 
−
| 3 || -0.14254654307
 
−
|-
 
−
| 4 || 1.15782128235
 
−
|-
 
−
| 5 ||-3.38051500625
 
−
|-
 
−
| 6 || -0.29100619138
 
−
|-
 
−
| 7 || 0.87144798272
 
−
|-
 
−
| 8 || -6.79971145522
 
−
|-
 
−
| 9 || -0.45231565944
 
−
|-
 
−
| 10 || 0.64836082745
 
−
|}
 
  
 
== Examples ==
 
== Examples ==
−
'''TAN(x)'''
+
'''ASIN(x)'''
−
*'''x  ''' is the angle in radians.
+
*'''x  ''' is the Number.
−
 
+
{| id="TABLE3" class="SpreadSheet blue"
−
{|id="TABLE1" class="SpreadSheet blue"
 
−
 
 
 
|- class="even"
 
|- class="even"
−
|'''TAN(Radian)'''
+
|'''ASIN(number)'''
−
|'''Value'''
+
|'''Angle(Radian)  '''  
−
 
 
 
|- class="odd"
 
|- class="odd"
−
| TAN(0)
+
| class="sshl_f " | ASIN(-0.8)
−
| 0
+
| class="sshl_f" | -0.9273
  
 
|- class="even"
 
|- class="even"
−
| TAN(1)
+
| class="sshl_f" | ASIN(1)
−
| 1.55740772465
+
| class="ssh1_f" | 1.5707963267948965
  
 
|- class="odd"
 
|- class="odd"
−
|TAN(90)
+
| class="sshl_f " | ASIN(0.559)
−
| -1.99520041221
+
| class="sshl_f" | 0.5931792803038736
  
 
|}
 
|}
  
  
−
==See Also==
+
{| id="TABLE3" class="SpreadSheet blue"
 +
|- class="even"
 +
| Complex(RN,IN,SF)
 +
! RN
 +
! IN
 +
! SF
 +
! RESULT
 +
|-
 +
|- class="odd"
 +
|Complex(5,6)
 +
|5
 +
|6
 +
|
 +
|5+6i
 +
|- class="even"
 +
|Complex(5,2,"j")
 +
|5
 +
|2
 +
|j
 +
|5+6j
 +
|- class="odd"
 +
| Complex(2,0,"i")
 +
|2                                     
 +
|0
 +
|i
 +
|2
 +
|- class="even"
 +
| Complex(0,-4,i)
 +
|0
 +
|4
 +
|i
 +
|4i
 +
|- class="odd"
 +
|Complex(5,"j")
 +
|5
 +
|
 +
|j
 +
|Error
 +
|}
  
−
*[[Manuals/calci/DTAN | DTAN]]
+
{|id="TABLE3" class="SpreadSheet blue"
−
 
+
!width="50"|Name
−
*[[Manuals/calci/ATAN | ATAN]]
+
!width="225"|Effect
−
 
+
!width="225"|Games Found In
−
==References==
+
|-
 +
|Poké Ball || Regular Poké Ball || All Versions
 +
|-
 +
|Great Ball || Better than a Poké Ball || All Versions
 +
|}
  
−
*[http://en.wikipedia.org/wiki/Trigonometric_functions List of Trigonometric Functions]
+
<math>\tilde{} </math>
−
*[http://en.wikipedia.org/wiki/Sine TAN]
 

Latest revision as of 05:34, 11 November 2013

Demo Study Page

  • Where x is the number and it is varying from -1 to 1.
  • The value of ASIN(x) is in radians in the range -pi()/2 to pi()/2.
  • Calci returns the value of arcsine (inverse sine)is in Radians.
  • The number can be a single value or any number of values.

For example, ASIN(0.5,(-0.2),1) gives the arcsine or inversesine values for each element.

Description

Consider x = (-0.8) then, ASIN((-0.8)) is -0.9273

  • This function is the Inverse function of Sin in trigonometry.
  • It's also called as Cyclometric function.
  • ASIN is described as Arcsin of a given number and denoted by (x).
  • In ASIN(x) ,x value should be with in -1 & 1.
  • To find the angle in degrees, multiply the result angle with 180/PI().
  • DEGREES function can also be used.

For example ASIN(-0.8)*180/PI() or DEGREES(ASIN(-0.8)) gives -53.13010235415598

Examples

ASIN(x)

  • x is the Number.
ASIN(number) Angle(Radian)
ASIN(-0.8) -0.9273
ASIN(1) 1.5707963267948965
ASIN(0.559) 0.5931792803038736


Complex(RN,IN,SF) RN IN SF RESULT
Complex(5,6) 5 6 5+6i
Complex(5,2,"j") 5 2 j 5+6j
Complex(2,0,"i") 2 0 i 2
Complex(0,-4,i) 0 4 i 4i
Complex(5,"j") 5 j Error
Name Effect Games Found In
Poké Ball Regular Poké Ball All Versions
Great Ball Better than a Poké Ball All Versions

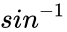Retrieved from "http://wiki.zcubes.com/index.php?title=Manuals/calci/COT&oldid=193340"