Difference between revisions of "Manuals/calci/AVERAGE"
Jump to navigation
Jump to search
| Line 6: | Line 6: | ||
*This function gives the Average for given set numbers. | *This function gives the Average for given set numbers. | ||
*Average means sum of all the given elements divided by Number of given elements. | *Average means sum of all the given elements divided by Number of given elements. | ||
| − | *It is also called Arithmetic mean. i.e if <math>n</math> numbers are given and each number is denoted by ai, where <math>i=1</math> to <math>n</math>, then <math>A.M=\frac{1}{n}\sum_{i=1}^n | + | *It is also called Arithmetic mean. i.e if <math>n</math> numbers are given and each number is denoted by ai, where <math>i=1</math> to <math>n</math>, then <math>A.M=\frac{1}{n}\sum_{i=1}^n ai</math>= 1/n(a1+a2+.....+an). |
*In this function N1,N2,... are either it can be numbers,arrays ,references of cells or | *In this function N1,N2,... are either it can be numbers,arrays ,references of cells or | ||
*we can enter the logical values directly. This function will show .the result as Error , | *we can enter the logical values directly. This function will show .the result as Error , | ||
| Line 17: | Line 17: | ||
*Mode: It is the most frequently repeated number in a given set of numbers. | *Mode: It is the most frequently repeated number in a given set of numbers. | ||
*E.g.The mode of 2,2,2,3,4,5 and 7 is 2 | *E.g.The mode of 2,2,2,3,4,5 and 7 is 2 | ||
| + | |||
| + | \sum_{k=1}^N k^2 | ||
==Examples== | ==Examples== | ||
Revision as of 23:09, 19 November 2013
AVERAGE(n1,n2,n3)
- Where are any real numbers.
Description
- This function gives the Average for given set numbers.
- Average means sum of all the given elements divided by Number of given elements.
- It is also called Arithmetic mean. i.e if numbers are given and each number is denoted by ai, where to , then = 1/n(a1+a2+.....+an).
- In this function N1,N2,... are either it can be numbers,arrays ,references of cells or
- we can enter the logical values directly. This function will show .the result as Error ,
- when the numbers are error values or text that cannot change in to numbers.
- Also if the distribution is symmetric, then we can use this function to find the central tendency.
- The three most common measures of central tendency are: A.M, Median,& Mode.A.M:
- It is calculating by adding the given set of numbers and divided by the count of the given set of numbers. *E.g:Average of 2,4,2,7,2,3 and 5 is 3.6
- Median: It is the middle number of a sorted list(Ascending order) of numbers.
- E.g:The median of 2,2,2,3,4,5,7 is 3
- Mode: It is the most frequently repeated number in a given set of numbers.
- E.g.The mode of 2,2,2,3,4,5 and 7 is 2
\sum_{k=1}^N k^2
Examples
- AVERAGE( 2, 3, 11, 13, 17, 26, 34, 47)=19.125
- AVERAGE(5,-2,7,8,11,20,25,-9)=8.125
See Also
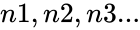 are any real numbers.
are any real numbers. numbers are given and each number is denoted by ai, where
numbers are given and each number is denoted by ai, where 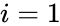 to
to 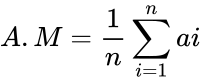 = 1/n(a1+a2+.....+an).
= 1/n(a1+a2+.....+an).