Difference between revisions of "Manuals/calci/EXP"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
<div style="font-size:30px">'''EXP(x)'''</div><br/> | <div style="font-size:30px">'''EXP(x)'''</div><br/> | ||
| − | *where x is the number . | + | *where <math>x</math> is the number . |
==Description== | ==Description== | ||
| − | *This function gives the e raised to the power of number. | + | *This function gives the <math>e</math> raised to the power of number. |
| − | *In EXP(x), where x represents the exponent of e, or e^x. | + | *In <math>EXP(x)</math>, where <math>x</math> represents the exponent of <math>e</math>, or <math>e^x</math>. |
| − | *The approximate value of the constant e=2.718281828459045 and it is equal to e^ | + | *The approximate value of the constant <math>e=2.718281828459045<math> and it is equal to <math>e^x</math> or <math>EXP(1)<math>. |
| − | *It is called the | + | *It is called the Mathematical Constant or Euler's Number or Napier's Constant. |
| − | * | + | *It is the base of natural logarithm. |
| − | + | *It can calculate the sum of infinite series: <math>e=1+(1/1)+(1/1.2)+(1/1.2.3)+(1/1.2.3.4) +...</math> | |
*And the inverse function of the natural logarithm function is the exponential function: | *And the inverse function of the natural logarithm function is the exponential function: | ||
| − | *f -1(x) = e^x. | + | *<math>f^{-1}(x) = e^x</math>. |
==Examples== | ==Examples== | ||
Revision as of 06:07, 21 November 2013
EXP(x)
- where is the number .
Description
- This function gives the raised to the power of number.
- In , where represents the exponent of , or .
- The approximate value of the constant or
- And the inverse function of the natural logarithm function is the exponential function:
- .
Examples
- EXP(1)=2.718281828459045
- EXP(0)=1
- EXP(-5)=0.0067379469990
- EXP(6.3)=544.5719101259
 is the number .
is the number .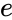 raised to the power of number.
raised to the power of number.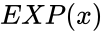 , where
, where 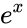 .
.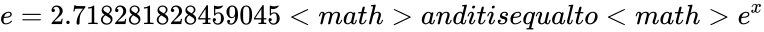 or
or 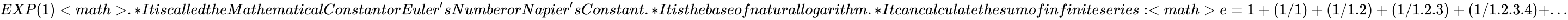
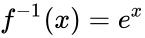 .
.