Difference between revisions of "Manuals/calci/CHITEST"
Jump to navigation
Jump to search
| Line 11: | Line 11: | ||
Each cell has an expected frequency of at least five. | Each cell has an expected frequency of at least five. | ||
*The <math>\chi^2</math> test first calculates a <math>\chi^2</math> statistic using the formula: | *The <math>\chi^2</math> test first calculates a <math>\chi^2</math> statistic using the formula: | ||
| − | <math>\chi^2 = \sum_{i=1}^{columns}\sum_{j=1}^{rows}\frac{ | + | <math>\chi^2 = \sum_{i=1}^{columns}\sum_{j=1}^{rows}\frac{{observed ij-expected ij}^{2}}}{grand total}</math> |
*observed ij is the array of the observed values in a given set of values | *observed ij is the array of the observed values in a given set of values | ||
*expected ij = column i total*row j total/grand total | *expected ij = column i total*row j total/grand total | ||
Revision as of 00:33, 25 November 2013
CHITEST(ar,er)
- is the array of observed values
- is the array of expected values
Description
- This function gives the the value from the chi-squared distribution. i.e it calculates statistic and degrees of freedom, then calls CHIDIST.
The conditions of test is
The table should be 2x2 or more than 2x2 Each observations should not be dependent All expected values should be 10 or greater. Each cell has an expected frequency of at least five.
- The test first calculates a statistic using the formula:
Failed to parse (syntax error): {\displaystyle \chi^2 = \sum_{i=1}^{columns}\sum_{j=1}^{rows}\frac{{observed ij-expected ij}^{2}}}{grand total}}
- observed ij is the array of the observed values in a given set of values
- expected ij = column i total*row j total/grand total
- observed and expected must have the same number of rows and columns and there must be atleast 2 values in each.
- A low result of is an indicator of independence.
- From the formula of we will get is always positive or 0.
- 0 only if observed ij=expected ij for each i and j.
- CHITEST uses the distribution with the number of Degrees of Freedom df.
where df=(r-1)(c-1),r>1 and c>1. If r=1 and c>1, then df = c-1 or if r>1 and c=1, then df=r-1. If r=c=1 then this function will give the error result
| Column1 | Column2 | Column3 | Column4 | |
| Row1 | 45 | 38 | 0.000313 | |
| Row2 | 10 | 23 | ||
| Row3 | 12 | 26 | ||
| Row4 | 40.5 | 49.36 | ||
| Row5 | 19.56 | 16.44 | ||
| Row6 | 17.05 | 17.41 |
Let’s see an example
B C
45 38
10 23
12 26
40.5 49.36
19.56 16.44
17.05 17.41
CHITEST (a, b)
i.e. =CHITEST (B2; C4, B5:C7) is 0.003
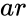 is the array of observed values
is the array of observed values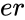 is the array of expected values
is the array of expected values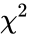 statistic and degrees of freedom, then calls CHIDIST.
statistic and degrees of freedom, then calls CHIDIST.