Difference between revisions of "Manuals/calci/LOG10"
Jump to navigation
Jump to search
| Line 4: | Line 4: | ||
*This function gives the logarithm value with the base 10. | *This function gives the logarithm value with the base 10. | ||
*The logarithm of x to base b is the solution y to the equation.i.e <math>b^y=x</math>. | *The logarithm of x to base b is the solution y to the equation.i.e <math>b^y=x</math>. | ||
| − | *For e.g The logarithm of 1000 to base 10 is 3. Because 1000=10*10*10=<math>10^3</math>. | + | *For e.g The logarithm of 1000 to base 10 is 3. Because 1000 = 10*10*10 = <math>10^3</math>. |
*The logarithm of base 10 is called Common Logarithm or Decimal Logarithm. | *The logarithm of base 10 is called Common Logarithm or Decimal Logarithm. | ||
*It is denoted by <math>\log_{10}</math> or <math>log(x)</math>. | *It is denoted by <math>\log_{10}</math> or <math>log(x)</math>. | ||
*<math>\log_{10}(x)</math> is related to the number of decimal digits of a positive integer x: the number of digits is the smallest integer strictly bigger than <math>\log_{10}(x)</math>. | *<math>\log_{10}(x)</math> is related to the number of decimal digits of a positive integer x: the number of digits is the smallest integer strictly bigger than <math>\log_{10}(x)</math>. | ||
| − | *For e.g:log(5260)=3.7209, that is nearly(next digit) to 4. | + | *For e.g:log(5260)= 3.7209, that is nearly(next digit) to 4. |
*That is the number of digits of 5260(4). | *That is the number of digits of 5260(4). | ||
Revision as of 02:52, 26 November 2013
LOG10(n)
- where is the positive real number.
Description
- This function gives the logarithm value with the base 10.
- The logarithm of x to base b is the solution y to the equation.i.e .
- For e.g The logarithm of 1000 to base 10 is 3. Because 1000 = 10*10*10 = .
- The logarithm of base 10 is called Common Logarithm or Decimal Logarithm.
- It is denoted by or .
- is related to the number of decimal digits of a positive integer x: the number of digits is the smallest integer strictly bigger than .
- For e.g:log(5260)= 3.7209, that is nearly(next digit) to 4.
- That is the number of digits of 5260(4).
Examples
=log 10(5)= 0.698970004 =log(55)= 1.740362689 =log(10)= 1 =log(1)= 0 =log(-10)= NaN =log(0.25)= -0.602059991
See Also
 is the positive real number.
is the positive real number. .
.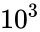 .
. or
or 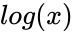 .
.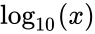 is related to the number of decimal digits of a positive integer x: the number of digits is the smallest integer strictly bigger than
is related to the number of decimal digits of a positive integer x: the number of digits is the smallest integer strictly bigger than