Difference between revisions of "Manuals/calci/MMULT"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''MMULT(a1, | + | <div style="font-size:30px">'''MMULT(a1,a2)'''</div><br/> |
| − | *where a1 and a2 the array if two matrices | + | *where <math>a1</math> and <math>a2</math> are the array if two matrices |
==Description== | ==Description== | ||
| − | *This function gives product of two matrices.Matrix multiplication is of two types: | + | *This function gives product of two matrices. |
| − | + | *Matrix multiplication is of two types: | |
| − | *For e.g. 4x2 matrix can multiply with 2x3. The matrix | + | Type 1: A scalar (a constant) is multiplied with the each element of the matrix. |
| + | Type 2: Multiplication of two matrices. | ||
| + | *We can do the matrix multiplication when the number of columns in the first matrix equals the number of rows in the second matrix. | ||
| + | *For e.g. 4x2 matrix can multiply with 2x3. The matrix product of two arrays <math>a</math> and <math>b</math> is <math>xij= \sum_{k=1}^n aik.bkj</math>, where <math>i</math> is the row number and <math>j</math> is the column number. | ||
*i.e Multiply the elements of each row of 1st matrix by elements of each column of 2nd matrix. | *i.e Multiply the elements of each row of 1st matrix by elements of each column of 2nd matrix. | ||
*So the resultant matrix of the order is:Rows of 1st matrix × Columns of 2nd. For e.g . | *So the resultant matrix of the order is:Rows of 1st matrix × Columns of 2nd. For e.g . | ||
Revision as of 04:24, 26 November 2013
MMULT(a1,a2)
- where and are the array if two matrices
Description
- This function gives product of two matrices.
- Matrix multiplication is of two types:
Type 1: A scalar (a constant) is multiplied with the each element of the matrix. Type 2: Multiplication of two matrices.
- We can do the matrix multiplication when the number of columns in the first matrix equals the number of rows in the second matrix.
- For e.g. 4x2 matrix can multiply with 2x3. The matrix product of two arrays and is , where is the row number and is the column number.
- i.e Multiply the elements of each row of 1st matrix by elements of each column of 2nd matrix.
- So the resultant matrix of the order is:Rows of 1st matrix × Columns of 2nd. For e.g .
- If we multiply a4x2 matrix with a 2x3 matrix, the product matrix is 4x3 .
- This function will give the result as error when:
- The number of columns in the 1st matrix is not equal to number of rows in the 2nd matrix.
- In the range cell, any cells are empty or that should not be convert in to numbers.
Examples
A student investigated the chance of getting viral fever in a school for a period that took vitamin tablets every day. The total number of students 880. In that 639 students didn't get viral fever and 241 students got fever .But the expected ratio is 1:3
Answer
- If the ratio is 1:3 and the total number of observed individuals is 880, then the expected numerical values should be: 660 will not get fever and 220 students will get fever.
| No Fever | Get Fever | |
|---|---|---|
| Observed Values | 639 | 241 |
| Expected Values | 660 | 220 |
| 0.668 | 2 |
- The value is 2.668
- Now
- From the Chi Squared Distribution probability table with is 1, the value of 2.668 is 0.10.
CHITEST(or,er) = 0.10
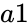 and
and 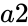 are the array if two matrices
are the array if two matrices and
and 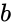 is
is 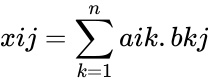 , where
, where 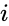 is the row number and
is the row number and 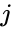 is the column number.
is the column number.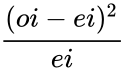
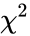 value is 2.668
value is 2.668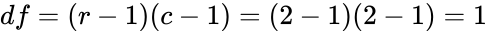
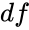 is 1, the
is 1, the