Difference between revisions of "Manuals/calci/CHITEST"
Jump to navigation
Jump to search
| Line 19: | Line 19: | ||
*0 only if <math>observed ij = expected ij</math> for each <math>i</math> and <math>j</math>. | *0 only if <math>observed ij = expected ij</math> for each <math>i</math> and <math>j</math>. | ||
*CHITEST uses the <math>\chi^2</math> distribution with the number of Degrees of Freedom df. | *CHITEST uses the <math>\chi^2</math> distribution with the number of Degrees of Freedom df. | ||
| − | + | *where <math>df=(r-1)(c-1),r>1</math> and <math>c>1</math>. | |
| − | + | *If <math>r=1</math> and <math>c>1</math>, then <math>df = c-1</math> or if <math>r>1</math> and <math>c=1</math>, then <math>df = r-1</math>. | |
If <math>r = c = 1</math> then this function will give the error result | If <math>r = c = 1</math> then this function will give the error result | ||
Revision as of 22:37, 26 November 2013
CHITEST(ar,er)
- is the array of observed values
- is the array of expected values
Description
- This function gives the the value from the chi-squared distribution and the appropriate degrees of freedom. i.e it calculates statistic and degrees of freedom, then calls CHIDIST.
The conditions of test is
The table should be 2x2 or more than 2x2 Each observations should not be dependent All expected values should be 10 or greater. Each cell has an expected frequency of at least five.
- The test first calculates a statistic using the formula:
- is the array of the observed values in a given set of values
- observed and expected must have the same number of rows and columns and there must be atleast 2 values in each.
- A low result of is an indicator of independence.
- From the formula of we will get is always positive or 0.
- 0 only if for each and .
- CHITEST uses the distribution with the number of Degrees of Freedom df.
- where and .
- If and , then or if and , then .
If then this function will give the error result
Examples
A student investigated the chance of getting viral fever in a school for a period that took vitamin tablets every day. The total number of students 880. In that 639 students didn't get viral fever and 241 students got fever .But the expected ratio is 1:3
Answer
- If the ratio is 1:3 and the total number of observed individuals is 880, then the expected numerical values should be: 660 will not get fever and 220 students will get fever.
| No Fever | Get Fever | |
|---|---|---|
| Observed Values | 639 | 241 |
| Expected Values | 660 | 220 |
| 0.668 | 2 |
- The value is 2.668
- Now
- From the Chi Squared Distribution probability table with is 1, the value of 2.668 is 0.10.
CHITEST(or,er) = 0.10
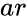 is the array of observed values
is the array of observed values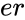 is the array of expected values
is the array of expected values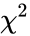 statistic and degrees of freedom, then calls CHIDIST.
statistic and degrees of freedom, then calls CHIDIST.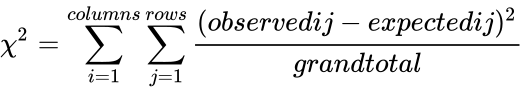
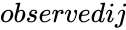 is the array of the observed values in a given set of values
is the array of the observed values in a given set of values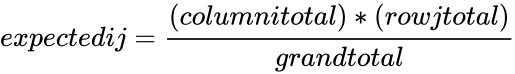
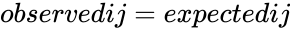 for each
for each 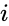 and
and 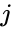 .
.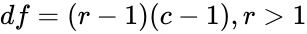 and
and 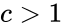 .
.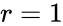 and
and 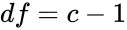 or if
or if 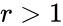 and
and 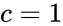 , then
, then 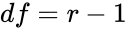 .
.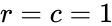 then this function will give the error result
then this function will give the error result
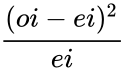
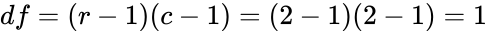
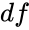 is 1, the
is 1, the